- Homework is due.
- I was talking with Neil about #35/36, p. 1086.
If you have a velocity field, then you have a means for obtaining paths of particles in the field. You just need to solve some differential equations....
- I was talking with Neil about #35/36, p. 1086.
- Your exam redos are due tomorrow.
- Sarah Stryffeler is giving a talk on Saturday, Nov. 14 at 2:15 in
GH 201. It concerns her work on measuring greenhouse gases. She will
also have a poster for OVSOT on Friday the 13th, and will be in the SU
ballroom presenting before class and after two.
Stop by and support her!
Anyone else presenting for the Kentucky Academy of Sciences?
- The line integral of $f$ along $C$ is
\[
\int_{C} f(x,y)ds = \lim_{n \to \infty}\sum_{i=1}^{n}f(x_i^*,y_i^*)
\Delta s
\]
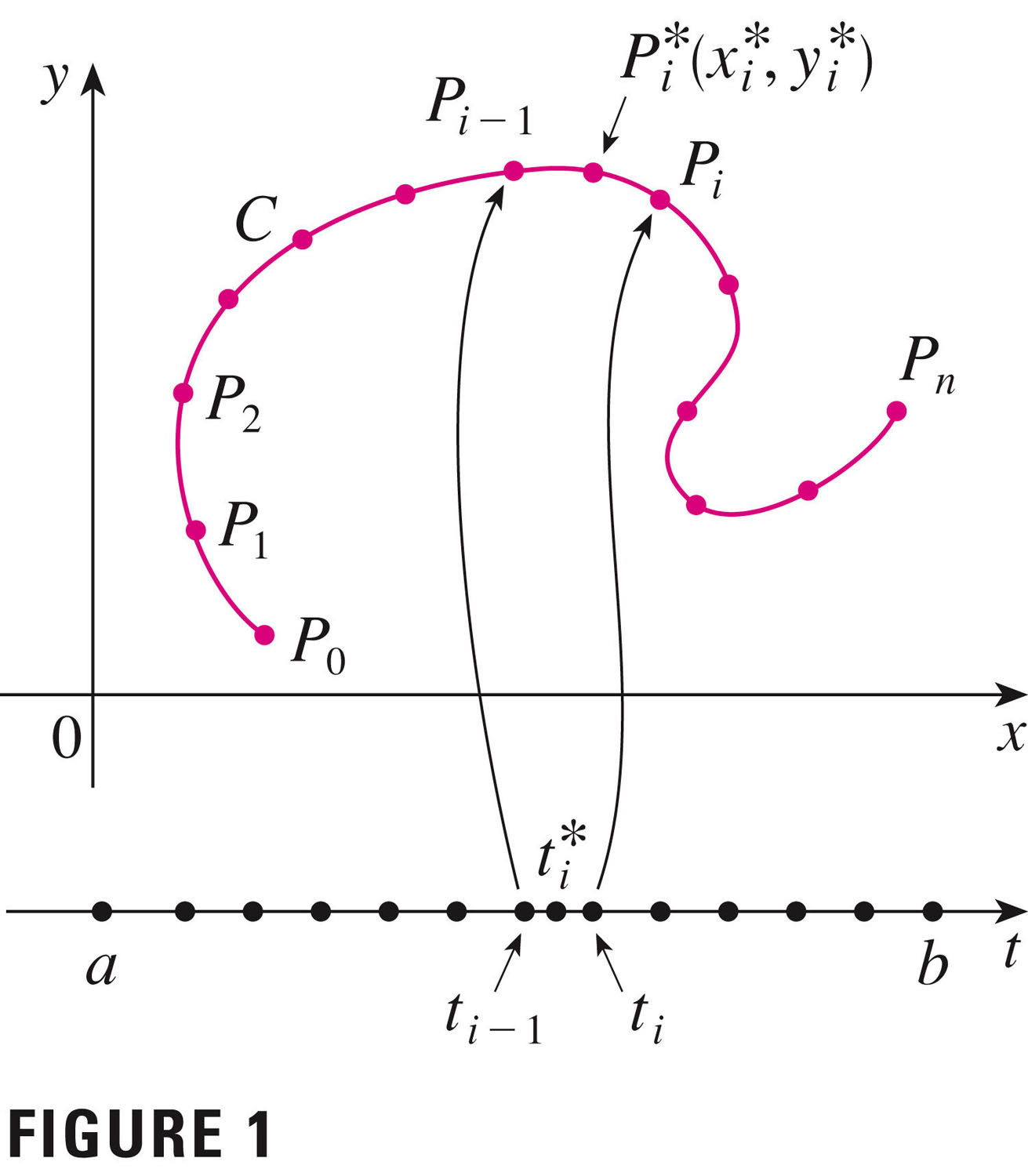
- If $f$ is continuous, then
\[
\int_{C} f(x,y)ds = \int_{a}^{b} f(x(t),y(t))
{\sqrt{\left(\frac{dx}{dt} \right)^2 +
\left(\frac{dy}{dt} \right)^2
}}
dt
\]
and this is independent of the parameterization $(x(t),y(t))$ (provided
the curve is traversed just once) as $t$ increases from $a$ to
$b$.
We can think of this as an area, per Figure 2 (if $f$ is positive):
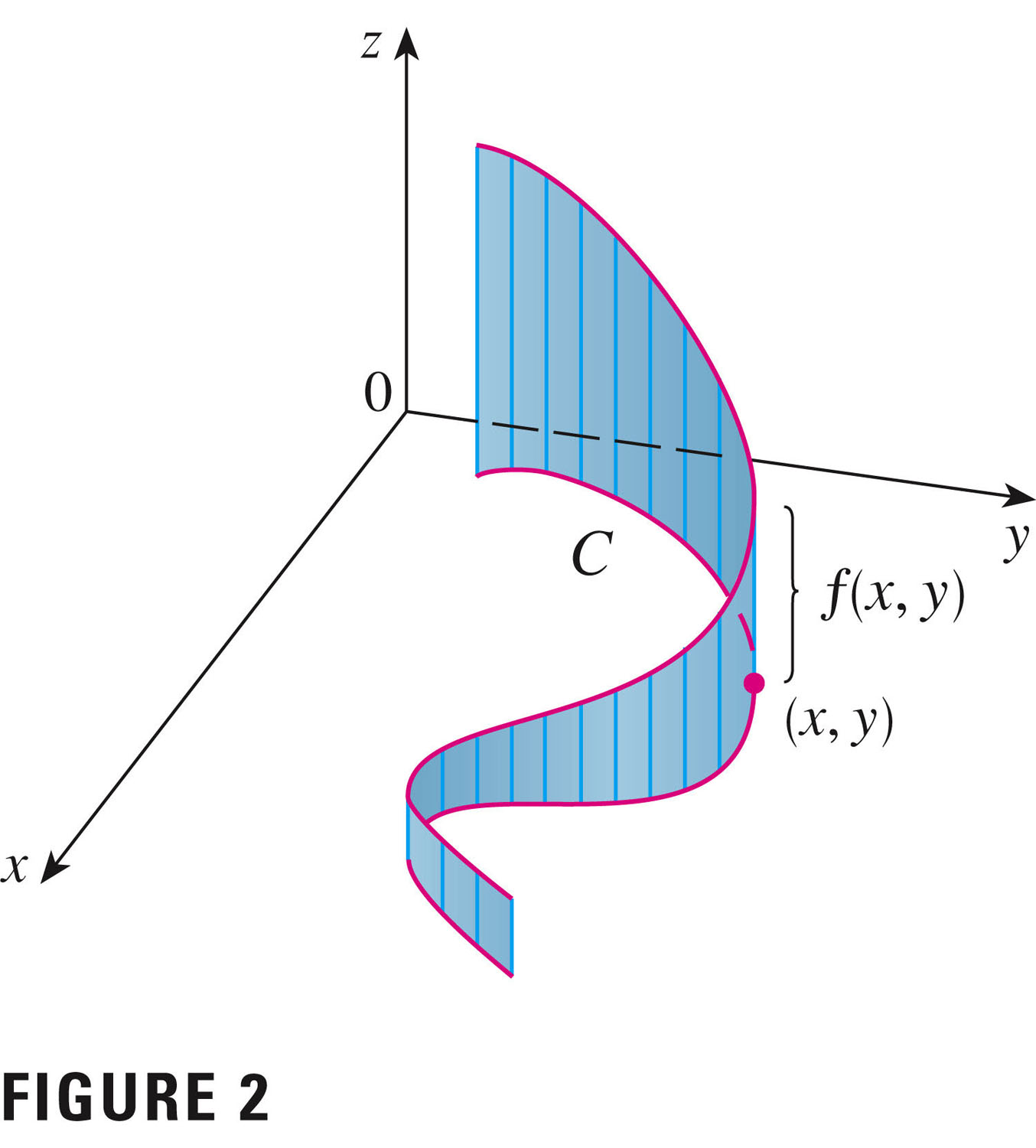
Although with $f(x,y)=1$ we can also think of this as the length of the curve. Note: we think of $dt$ as positive (and it is, because we've specified the orientation). But if we reverse the orientation, we'd need to "reverse $dt$" as well.
- Rather than look at line integrals along the curve $C$, with differential $ds$, we could integrate components along the $x$ and $y$ directions: line integrals of $f$ along $C$ with respect to $x$ and $y$ are \[ \int_{C} f(x,y)dx = \int_{a}^{b} f(x(t),y(t)) x^{'}(t) dt \] and \[ \int_{C} f(x,y)dy = \int_{a}^{b} f(x(t),y(t)) y^{'}(t) dt \]
- Let's look at Example 4 first, then take on #8, p. 1096.
Example 4, p. 1091,
- raises the issue of orientation;
- illustrates two different strategies of parameterization;
- telegraphs a topic of section 16.3: path independence of line integrals.
- We can think of re-think this one as a vector field problem.
- Examples:
- #8, p. 1096 (with lots of extra detail)
- #12 (3-d versions of all of this is no big deal)
- Now we want to extend our line integrals to vector fields.
First of all, let's get oriented: instead of thinking of the position as given by a point, we'll indicate it by a position vector, with starts at the origin and has its tip at the point of interest:
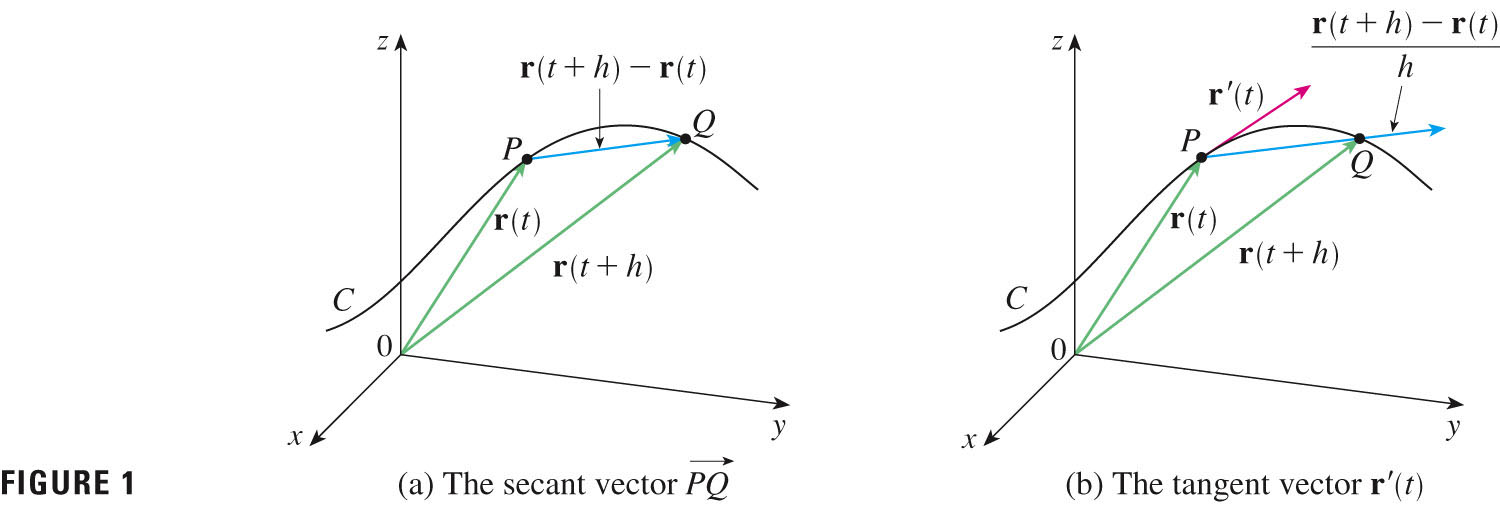
Then $d{\bf{r}}=\langle dx,dy,dz\rangle$, in particular.
Let ${\bf{F}}$ be a continuous vector field defined on a smooth curve $C$ traced out by the vector function ${\bf{r}}(t)$, $a \le t \le b$. Then the line integral of ${\bf{F}}$ along $C$ is \[ \int_{C} {\bf{F}}({\bf{r}}(t)) \cdot d{\bf{r}} = \int_{C} {\bf{F}}({\bf{r}}(t)) \cdot {\bf{r}}^{'}(t) dt \]
If vector field ${\bf{F}}=P\hat{i}+Q\hat{j}+R\hat{k}$=$\langle P,Q,R \rangle$, then we can break the integral into three: \[ \int_{C} {\bf{F}} \cdot d{\bf{r}} = \int_{C} Pdx + Qdy + Rdz \] since $d{\bf{r}}=\langle dx,dy,dz\rangle$. With my parentheses fascination, you can be sure that I'd like to put parentheses around that last integrand: $\int_{C} (Pdx + Qdy + Rdz)$ -- just to emphasize that the integration is over all....
- #32, p. 1097
- #52
We'll start by thinking of the very important problem of the conservation of energy, p. 1105.