- Your exams are returned.
- The exam
- Once again, you may redo the exam, by Friday, for 40% of
the points you missed. That enables everyone to get to a C or
better.
Print off a new copy. Submit it (only do those which weren't full credit last time) and your original on Friday.
You're free to discuss it with anyone.
Everyone scoring below 35 needs to see me to discuss their exam at some point, either before or after resubmitting -- your choice. I'm going to hold your redo points hostage until you also pay me a visit!
- Individual comments:
- Unconstrained optimization (but you need to check the boundary). Use symmetry.
- Constrained optimization (but you can use what you know about hyperboloids to do it without Lagrange multipliers!). Use symmetry.
- #3
- separable, straightforward
- mask (1,1;1,1)
- mask (1,2,1;2,4,2;1,2,1) -- most of the function values are zero!
- It's a piece of pie -- a polar rectangle.
- Straightforward -- you've just got to get the limits of integration right. Use symmetry.
- General comments:
- Some of you integrate positive integrands over
positively oriented domains and get 0 or negative
stuff. That indicates that you're missing something
critical about integration!
- Some of you need to know a little more about sine. At least the easiest special angles....
- Some of you integrate positive integrands over
positively oriented domains and get 0 or negative
stuff. That indicates that you're missing something
critical about integration!
- The exam
- The line integral of $f$ along $C$ is
\[
\int_{C} f(x,y)ds = \lim_{n \to \infty}\sum_{i=1}^{n}f(x_i^*,y_i^*)
\Delta s
\]
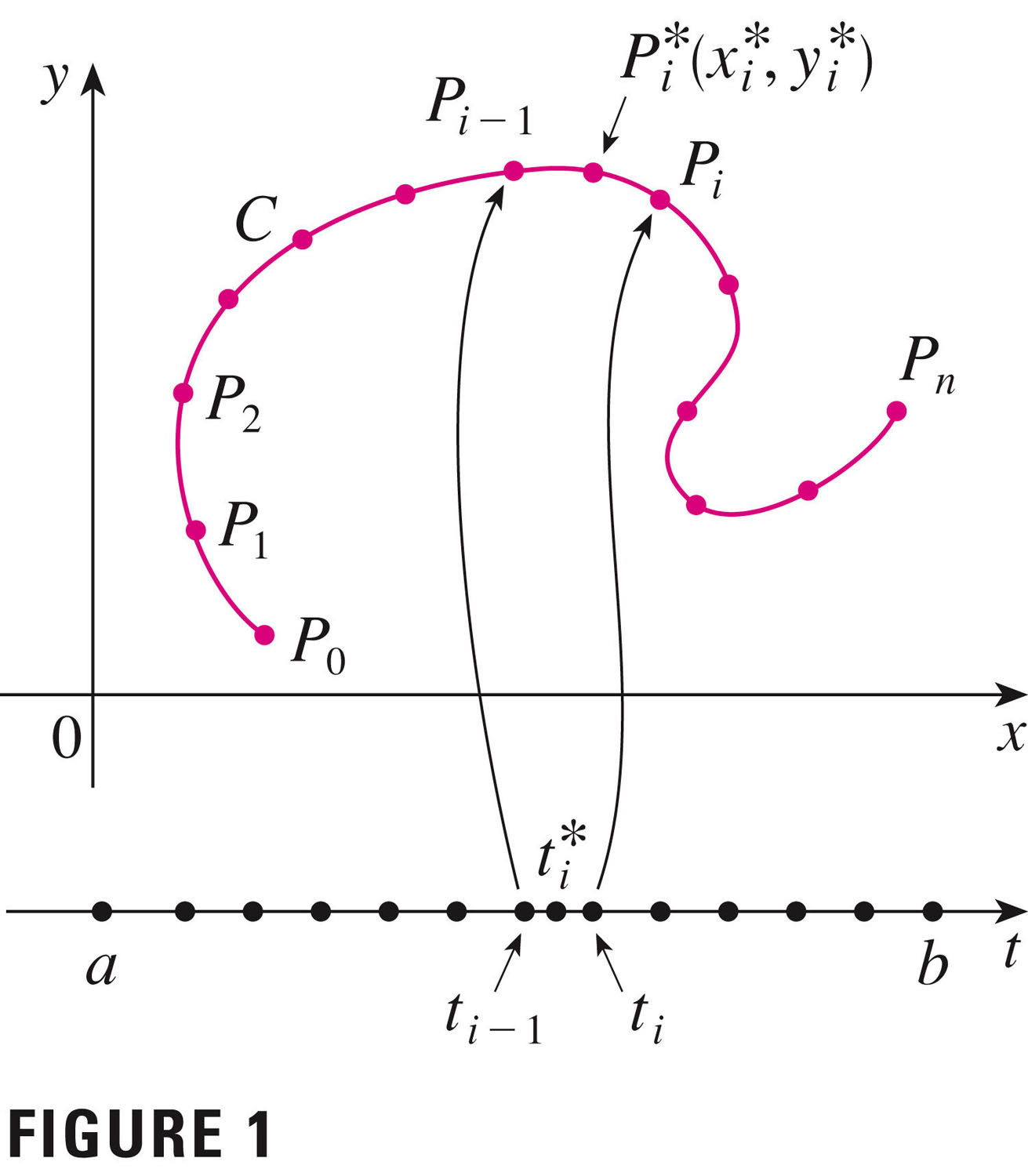
- If $f$ is continuous, then
\[
\int_{C} f(x,y)ds = \int_{a}^{b} f(x(t),y(t))
{\sqrt{\left(\frac{dx}{dt} \right)^2 +
\left(\frac{dy}{dt} \right)^2
}}
dt
\]
and this is independent of the parameterization $(x(t),y(t))$ (provided
the curve is traversed just once) as $t$ increases from $a$ to
$b$.
We can think of this as an area, per Figure 2 (if $f$ is positive):
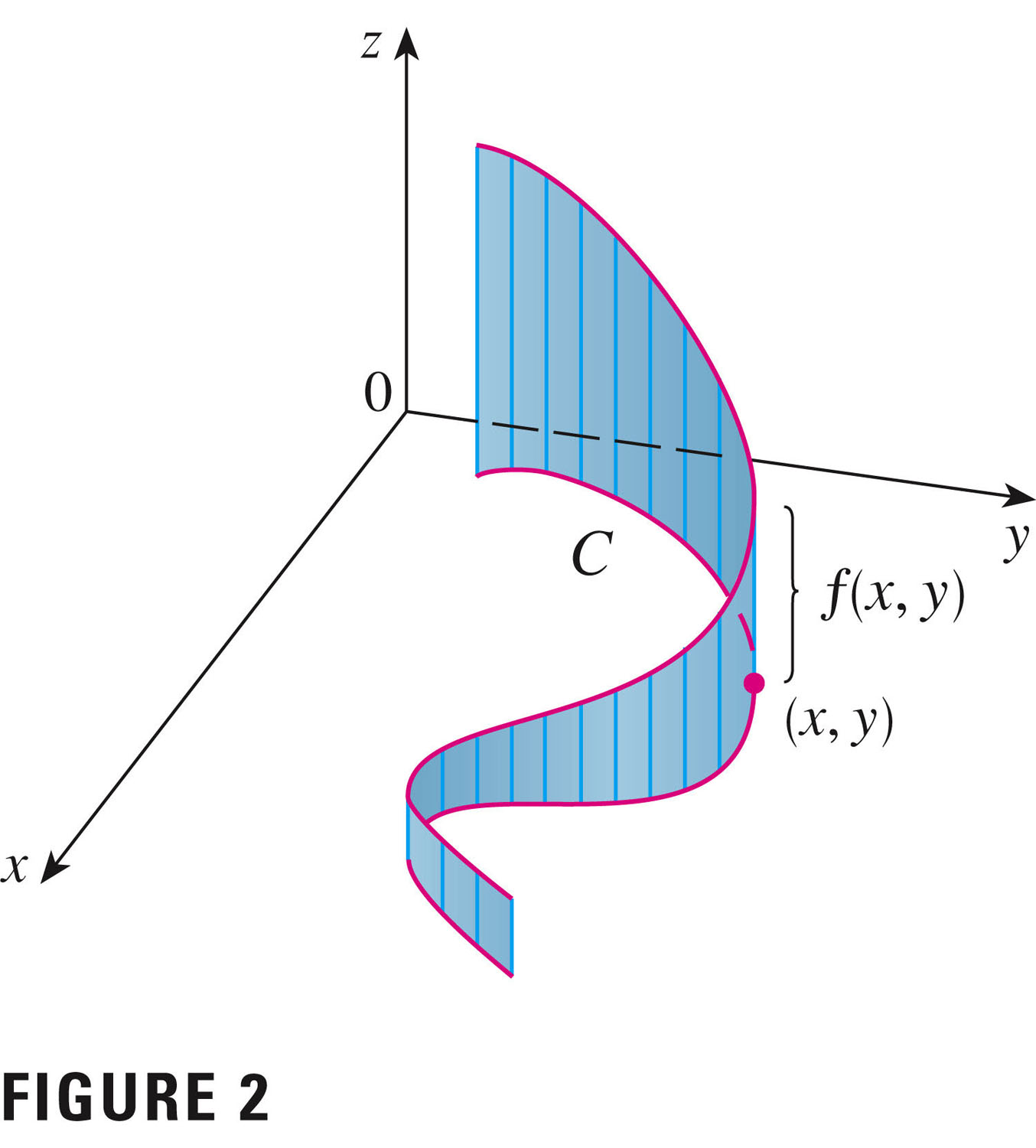
Although with $f(x,y)=1$ we can also think of this as the length of the curve. Note: we think of $dt$ as positive (and it is, because we've specified the orientation). But if we reverse the orientation, we'd need to "reverse $dt$" as well.
- Rather than look at line integrals along the curve $C$, with differential $ds$, we could integrate components along the $x$ and $y$ directions: line integrals of $f$ along $C$ with respect to $x$ and $y$ are \[ \int_{C} f(x,y)dx = \int_{a}^{b} f(x(t),y(t)) x^{'}(t) dt \] and \[ \int_{C} f(x,y)dy = \int_{a}^{b} f(x(t),y(t)) y^{'}(t) dt \]
- Let's look at Example 4 first, then take on #8, p. 1096.
Example 4, p. 1091,
- raises the issue of orientation;
- illustrates two different strategies of parameterization;
- telegraphs a topic of section 16.3: path independence of line integrals.
- We can think of re-think this one as a vector field problem.
- Examples:
- #8, p. 1096 (with lots of extra detail)
- #12 (3-d versions of all of this is no big deal)
- Now we want to extend our line integrals to vector fields.
Let ${\bf{F}}$ be a continuous vector field defined on a smooth curve $C$ traced out by the vector function ${\bf{r}}(t)$, $a \le t \le b$. Then the line integral of ${\bf{F}}$ along $C$ is \[ \int_{C} {\bf{F}}({\bf{r}}(t)) \cdot d{\bf{r}} = \int_{C} {\bf{F}}({\bf{r}}(t)) \cdot {\bf{r}}^{'}(t) dt = \int_{C} {\bf{F}} \cdot {\bf{T}} ds \] where ${\bf{T}}$ is the tangent vector (the component of velocity in the direction tangential to the motion).
If vector field ${\bf{F}}=P\hat{i}+Q\hat{j}+R\hat{k}$=$\langle P,Q,R \rangle$, then we can break the integral into three: \[ \int_{C} {\bf{F}} \cdot d{\bf{r}} = \int_{C} Pdx + Qdy + Rdz \] With my parentheses fascination, you can be sure that I'd like to put parentheses around that last integrand: $\int_{C} (Pdx + Qdy + Rdz)$ -- just to emphasize that the integration is over all....
Examples:
- #32
- I want to build up to #52.