- Homework 16.4 is due Thursday, your last homework to
submit.
- Homework 16.3 is returned. Graded #4, 6, 20.
- #4: conservative, and you found $f(x,y)$, for the most part.
- #6: not conservative
- #20: -2! A lot of you messed up your trig stuff to get 0....
You could get the right answer in two different ways:
- Laura
- Madison
- Something for Ada, from Richard Feynman (The Feynman lectures on
Physics, Volume II, p. 4-4)
- But see p. 1105 in our text.
Last time we looked at some important concepts, such as cross-products, that you may be unfamiliar with. Curl and divergence rely on two vector products (cross and dot), and an understanding of operators (which may be unfamiliar).
- We'll start with the cross-product:

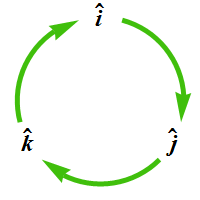

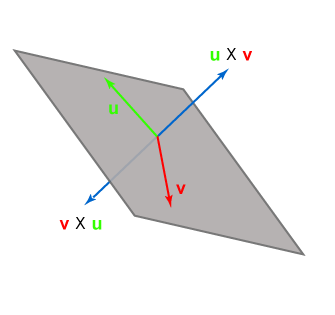
There are a few other properties of the cross-product that you should know:

- Let's begin getting serious by introducing the del operator:
\[
\nabla = \frac{\partial}{\partial x} {\bf{i}} +
\frac{\partial}{\partial y} {\bf{j}} +
\frac{\partial}{\partial z} {\bf{k}}
\]
We've seen $\nabla$ before, of course: when it acts on a scalar function $f$,
it returns the gradient of $f$, $ \nabla f$.
There are three ways that we use $ \nabla$:
- as an operator (which is a type of function, which takes functions as
arguments, rather than numbers). This is exemplified by the gradient, but also
by the Laplacian (described below).
Quoting again from Feynman (VII, p. 2-6): operators are, "...as Jeans said, 'hungry for something to differentiate.'"
- since we've represented del as a vector, we might use it to
multiply vector functions -- applying both of the two types of
vector multiplication (dot- and cross-products) -- and returning
functions.
- applied with the dot-product, $\nabla$ creates a scalar function;
- applied with the cross-product, $\nabla$ creates a vector function.
- as an operator (which is a type of function, which takes functions as
arguments, rather than numbers). This is exemplified by the gradient, but also
by the Laplacian (described below).
- Curl of vector field ${\bf{F}}=\langle P,Q,R \rangle$:
\[
{\textrm{curl}}{\ \bf{F}} =
\left(
\frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z}
\right)
{\bf{i}}
+
\left(
\frac{\partial P}{\partial z} - \frac{\partial R}{\partial x}
\right)
{\bf{j}}
+
\left(
\frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y}
\right)
{\bf{k}}
\]
If curl ${\bf{F}} = {\bf{0}}$ at a point, then ${\bf{F}}$ is said to be
irrotational at that point:
Making use of $\nabla$, then, and the cross-product $\times$, we have
${\textrm{curl}}{\ \bf{F}} =\nabla \times {\bf{F}}$ We can use Green's theorem to try to understand the curl as rotation:
Start by switching to 2D (so F has no $z$-component). Then imagine a contour around a point, say a circle centered at the point, which is shrinking down to nothing. The picture is in your book, on page 1118 (without the shrinking part):
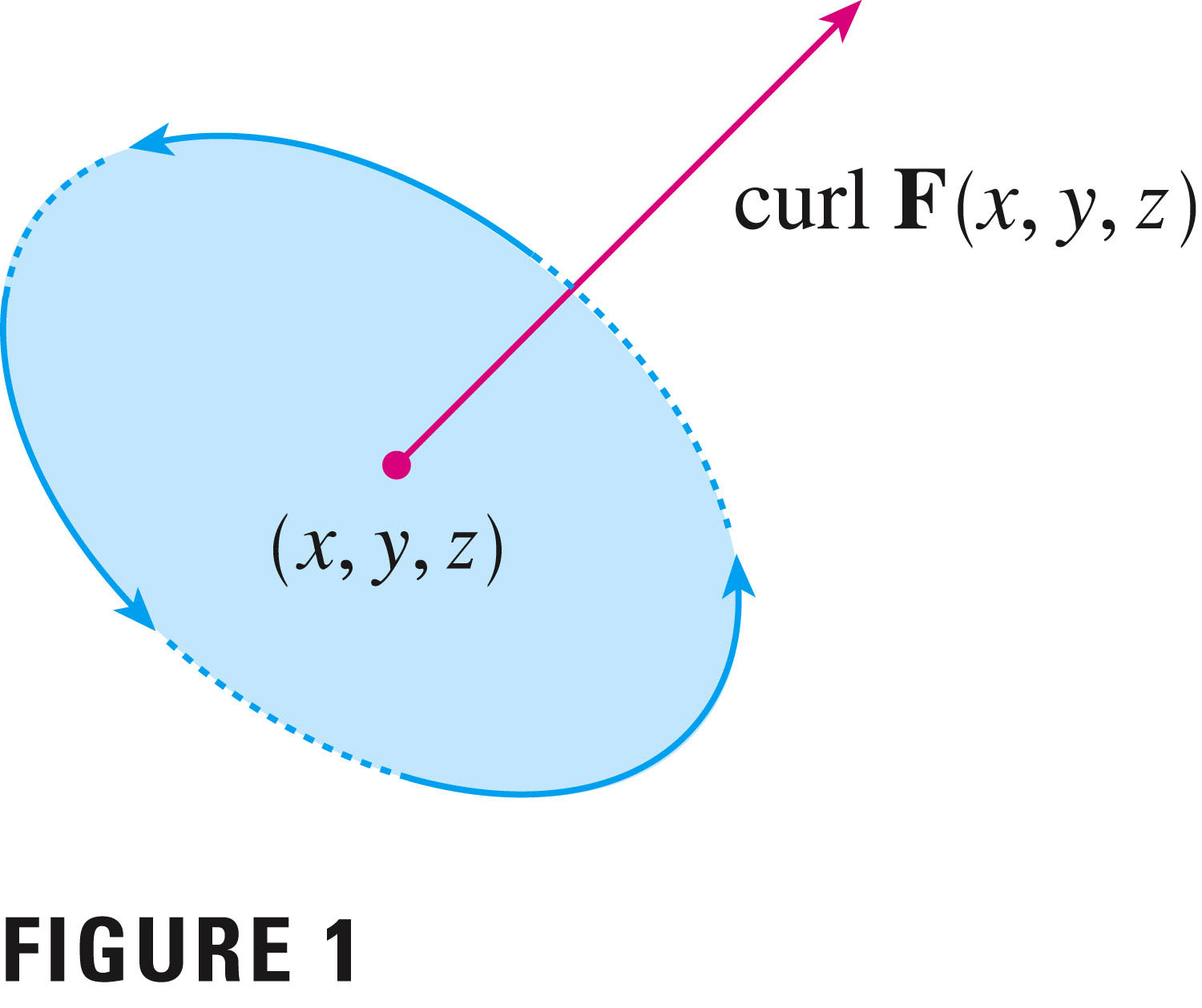
In the limit as the size of the circle shrinks to zero,
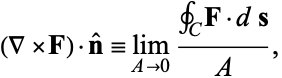
(Think about our quiz.)
Q: What if $\bf{F}$ is conservative, i.e. a gradient field?
If $f$ is a function of three variables that has continuous second-order partial derivatives on disk $D$, then \[ {\textrm{curl}}(\ \nabla f) = {\textrm{curl}}\ {\bf{F}} = {\bf{0}} \] (note that that's a vector ${\bf{0}}$). This says that if ${\bf{F}}$ is conservative, then curl ${\bf{F}} = {\bf{0}}$.
This falls right out of the curl equations: \[ {\textrm{curl}}{\ \bf{F}} = \left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z} \right) {\bf{i}} + \left( \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x} \right) {\bf{j}} + \left( \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) {\bf{k}} \]
where $P=f_x$, $Q=f_y$, and $R=f_z$.
The proof is by Clairaut's theorem (generalized to 3D). Recall: Suppose $f$ is defined on a disk $D$ that contains the point $(a,b)$. If the functions $\frac{\partial^2 f}{\partial x \partial y}$ and $\frac{\partial^2 f}{\partial y \partial x}$ are both continuous on $D$, then \[ \frac{\partial^2 f}{\partial x \partial y} = \frac{\partial^2 f}{\partial y \partial x} \]
The components of the curl are differences of mixed partials, as you've perhaps noticed. Hence, the curl of a gradient field is zero.
Theorem 4, p. 1117: If ${\bf{F}}$ is a vector field defined on all of $\Re^3$ whose component functions have continuous partial derivatives and ${\textrm{curl}}{\ \bf{F}} = {\bf{0}}$, then ${\bf{F}}$ is a conservative vector field.
- Divergence:
\[
{\textrm{div}\ \bf{F}} =
\frac{\partial P}{\partial x} +
\frac{\partial Q}{\partial y} +
\frac{\partial R}{\partial z}
= \langle \frac{\partial }{\partial x},
\frac{\partial }{\partial y},
\frac{\partial }{\partial z} \rangle \langle P,Q,R \rangle
= \nabla \cdot {\bf{F}}
\]
Note that this is a scalar function, which measures the tendency of the vectors of $\bf{F}$ to flow out of (or into) a point.
If ${\textrm{div}\ \bf{F}} = 0$, then ${\bf{F}}$ is said to be incompressible.
Examples:
- #7, p. 1121
- #9-11
- The Laplacian operator is designated by $\nabla^2$, and creates a
scalar function from a scalar function. We can think of this as the dot
product -- a scalar -- of two vectors:
\[
\nabla^2 f = \nabla \cdot \nabla f
=
\frac{\partial^2 f}{\partial x^2}+
\frac{\partial^2 f }{\partial y^2}+
\frac{\partial^2 f }{\partial z^2}
\]
Solutions of Laplace's equation $\nabla^2 f = 0$ are called harmonic functions, and are very important in physics and complex analysis.
- Examples: now that we've got all the machinary in place, let's
look at a couple of examples:
- #12, p. 1121
- #19: it turns out the $div\ curl{\bf{F}}=0$ -- p. 1119 -- again by Clairaut.
- #21: check curl
- #22: check div
- Maxwell's
equations should be the poster child for this section.
From the 11/22/2015 edition of the Guardian: Maxwell's equations: 150 years of light: "A century and a half ago, James Clerk Maxwell submitted a long paper to the Royal Society containing his famous equations. Inspired by Michael Faraday's experiments and insights, the equations unified electricity, magnetism and optics. Their far-reaching consequences for our civilisation, and our universe, are still being explored."
Light, electricity, and magnetism are brought together in these equations of physics.
Examples:
- #29 (we need this for #38)
- A rule for cross-products in general: ${\bf{A\times (B \times C)=B(A\cdot C)- (A\cdot B)C}}$
- #38 (Maxwell!)
- #37 (just to see curl in action)
- #29 (we need this for #38)