- Your first assignment is returned.
A couple of thoughts:
- Problem 1:
- Probabilities are numbers between 0 and 1.
- Probabilities are best left as fractions -- you don't need to turn them into decimals.
- Problem 2:
- Just stuff out of your first reading. Review that!
- Major issue: focus on outcomes for the rolls (there are 36),
rather than outcomes for the sums.
The difference is that each roll is equally likely, but each sum is not. (And, by the way, there are only 11 sums -- 2 to 12).
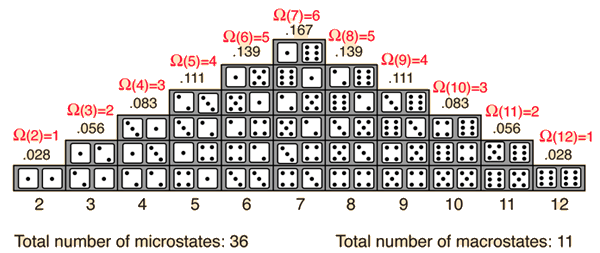
You can only do probability by counting when the outcomes are all equally likely.
- Problem 3:
What's the smallest sum you can get with three dice?
- Problem 4:
- Birth Month, not Birth Day
- Is it remarkable that in a room with five people, it's much more likely than not that two share a birth month? It's nearly twice as likely as not.
- Problem 1:
- I've tallied your votes for the top three topics from our
textbook. There are two clear winners, and a three-way tie for
third. So I made an executive decision about third place, and went with
the one that I think people will find the most interesting (and
useful): commuting.
Winners:
- The Loneliest Numbers
- Loves Me, Loves Me Not
- Commuting
- You have a reading assignment for next time: Chances Are (p. 183).
It's one of the more challenging readings, but it is tremendously important for anyone who ever gets a medical test (e.g. breast cancer screening, or prostate cancer screening -- so that covers about everyone!). Here we are being all practical again....
- When we increase the number of doors in the Monty Hall problem,
the situation gets worse and worse for the sticker. If there are ten
doors, then the probability that a sticker wins is 1/10, whereas the
probability for a switcher is 9/10 (complementary probabilities).
If there are N doors, then the probability that a sticker wins is
, whereas the probability for a switcher is
.
- In our next step, we changed the game a lot. The rules are:
- Five doors.
- Behind two of the doors are cars; behind the other three are donkeys.
- You pick two doors.
- You receive "a new car!" if either door you pick has a car behind it.
- Monty Hall looks at the other three doors, and shows one that has a donkey behind it. Then he offers you the two other doors for your two. Do you switch?
Our story so far:
- Suppose you picked doors 1 and 2.
- We used a tree to get the universe of possible placements
of the cars (and donkeys):
summary
- Now suppose that you receive a car only if you find
BOTH cars behind your two doors.
How does the problem change? (There's something dramatically new here!)
- What's the universe? (Did it change?)
- Which outcomes result in a win for sticking?
- Which outcomes result in a win for switching?
- What are the probabilities?
- What is dramatically different about these probabilities?
We learn something of that, anyway -- at least about six fish. But
We learn that
- "...numbers are shortcuts for counting by ones...." (p. 5)
- Furthermore, "...Humphrey might realize he can keep counting forever." (p. 5) -- something that will be very important when we come to talk about infinity.
Did you notice Humphrey using any other cues to help him keep track of the number of fish?
The triangle was known long before Pascal, however: on one side of your handout, you'll see a Chinese version of our triangle. On the other side you have a hexagonal tiling of the paper, that we can use to make a nice version of Pascal's triangle.
This is a famous bit of mathematics that some of you may recognize, and we'll study it throughout the course.
Suffice it to say, however, that Pascal studied it because he was interested in computing probabilities. This is a Pascal's probability calculator. Today we'll see how it is constructed; then we'll use it throughout the course.
Interestingly enough, there's a mistake in one row of the Chinese version of this table. Can you find it?
One thing that Pascal's triangle allows us to do: it allows us to understand how this Chinese culture of the 13th century wrote its numbers (Chinese Bamboo Counting Rods). How did these people write 15? 28? 30?