- You have a new probability assignment, due Friday. Come with questions about it on Wednesday (in other words, start early!).
Your reading for today (hopefully you've read it) is another attempt to convince you that probability is all about counting.
Question of the Day: What happens when you're falsely accused of doping at work?
Another thing our reading emphasizes is how bad "the experts" really are at probabilities. We rely on them, but maybe we shouldn't when it comes to risk.

and here's the result of doing that over and over:

How do we use it to carry out probability problems?
Last time we saw how the triangle can be used to count the universe of possible events. We looked at the row
and saw how we could use it to answer the question
We can interpret the numbers in that row as the number of ways of putting
- all in car one (and none in car two);
- 4 in car one, and 1 in car two;
- 3 in car one, and 2 in car two;
- 2 in car one, and 3 in car two;
- 1 in car one, and 4 in car two;
- none in car one (and all in car two)
So here are some typical probabilities, based on that row of Pascal's triangle:
- In how many distinctly different ways can we put 5 people into 2 cars?
(this is the size of the universe) - What's the probability that we put 2 in car one, and 3 in car two?
(now we're counting: that is, counting using Pascal's triangle) - What's the probability that we put everyone one in a single car?
(count again -- and it's figuring out which occurrences to count!) - What's the probability that no one is alone in a car?
(use the complement!)
This reading concerns "conditional probability", which is the probability of an event given that some other event has already occurred. So it's sort of a "probability within a probability" problem, and that just seems to make them twice as hard! But bear with me, and we'll see if we can't follow Strogatz as he attempts to turn what seems difficult into something reasonable, through "right thinking".
Well, right away our author does something regrettable -- he says that "...the probability that your friend will forget to water it is 30 percent." That's the chance that your friend will forget to water it, right? The probability is .30. So I want you to convert throughout: when Strogatz gives a probability as a percentage, you convert it to a decimal (or fraction).
Let's consider "the plant problem":
- Before going on vacation for a week, you ask your spacy friend to
water your ailing plant. Without water, the plant has a 90 percent
chance of dying. Even with proper watering, it has a 20 percent chance
of dying. And the probability that your friend will forget to water it
is 30 percent.
- What's the chance that your plant will survive the week?
- If it's dead when you return, what's the chance that your friend forgot to water it?
- If your friend forgot to water it, what's the chance that it'll be dead when you return?
- We usually start by defining some things. For example we could let
-
- the plant died
-
- the plant was watered
then, of course, we have also defined the complements:
-
- the plant didn't die
-
- the plant was not watered
-
- Let's start by considering the universe. We'll represent it in a
slightly different way, however, using a table. The first problem to
consider is the problem of the plants, living or dead, and the watering
(done or not). Because there are these two ways of looking at the
situation of our plants and their waterings, our universe will be
divided into two separate worlds....
- Venn diagrams, and
- a Table.
- Next we need to introduce this notion of conditional
probabilities. They're a kind of "side bet". You reduce your focus to
just a part of the universe, the part that has already come to
pass. Here's how we write them: for example,
The robability of
given
is written as
Now our author mentions "Bayes's Theorem", and, just so you know what that is, here it is. It relates the conditional probabilities to the probability that both of two different things happen in a set:
And because the order of the intersection (both happening) doesn't matter, the problem is symmetric in D and W:
These are useful, provided we know two of the three quantities -- then we can solve for the third.
And since the two quantities on the left-hand sides are equal, we can equate the right-hand sides:
This is Bayes's Theorem (and is especially useful provided we know three of the four quantities -- then we can solve for the fourth).
The given probabilities are
-
- We can now turn the English questions posed at the beginning of
the plant experiment into the following probabilities:
- What's the chance that your plant will survive the week?
- If it's dead when you return, what's the chance that your
friend forgot to water it?
- If your friend forgot to water it, what's the
chance that it'll be dead when you return?
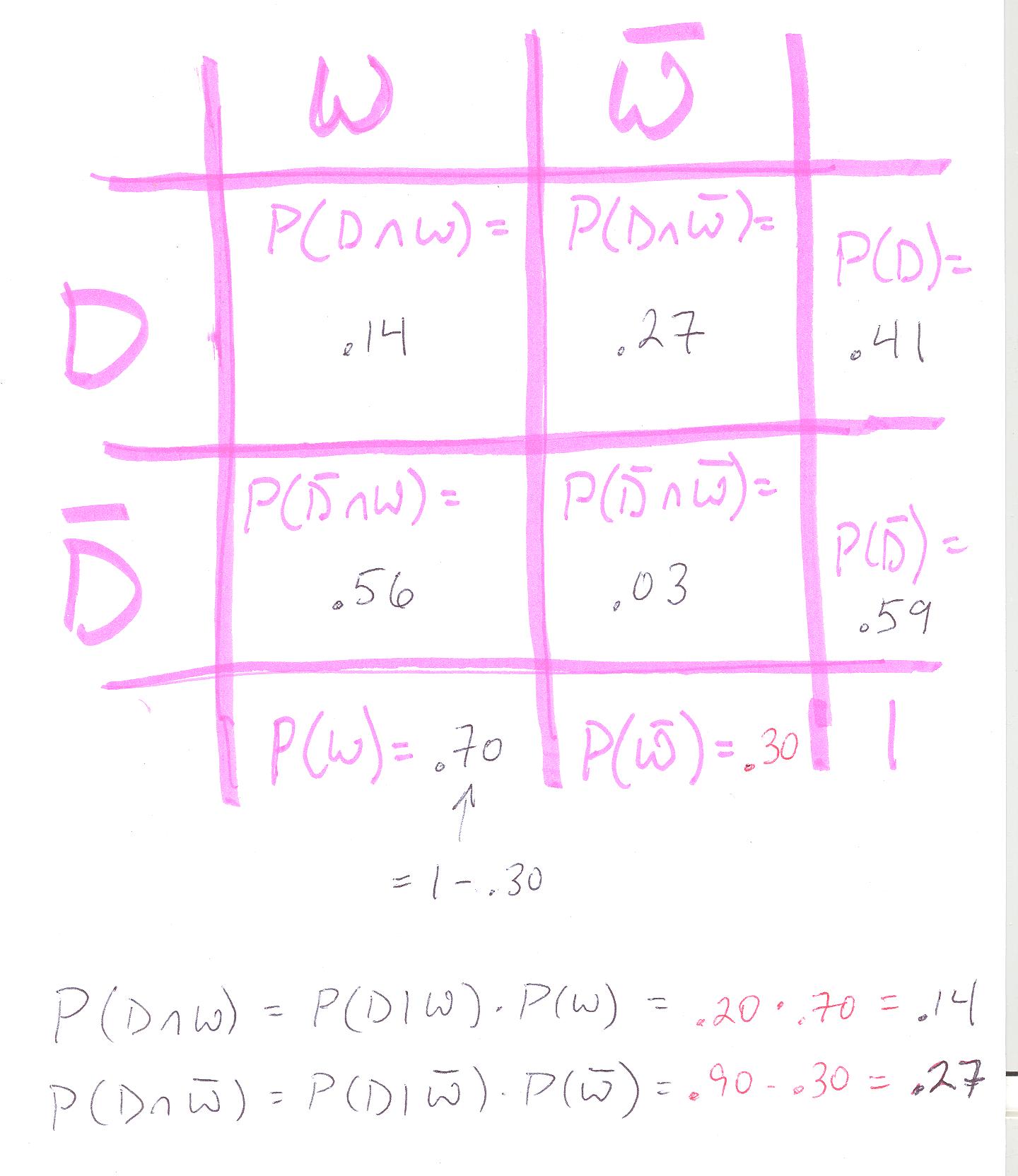
- What's the chance that your plant will survive the week?
- Now our author suggests that, rather than go through all this
convoluted stuff, we think in terms of "natural frequencies". Let's
see if we get the same answer any easier. Let's assume that there are
100 plants in the experiment, all either dead or not-dead, watered or
not-watered.
Once again, we'll use a Table.
"Gigerenzer and his colleagues asked doctors in Germany and the United States to estimate the probability that a woman with a positive mammogram actually has breast cancer, even though she's in a low-risk group: 40 to 50 years old, with no symptoms or family history of breast cancer.
"The probability that one of these women has breast cancer is 0.8 percent. If a woman has breast cancer, the probability is 90 percent that she will have a positive mammogram. If a woman does not have breast cancer, the probability is 7 percent that she will still have a positive mammogram. Imagine a woman who has a positive mammogram. What is the probability that she actually has breast cancer?"
We'll use "natural frequencies" to solve this problem.
- Let's start by considering the universe. The best way to represent it is as a table.
- Then we write down our givens:
-
- Then we solve for the unknown, which is
We can also fill in the rest of our table, and do other probabilities.
- Now that we've calculated the exact values, what do you think of
this quote from our text:
"As for the American doctors, ninety-five out of a hundred estimated the woman's probability of having breast cancer to be somewhere around 75 percent."
What are the consequences for your health care?
- Notice the difference between the German doctors and the American
doctors:
- 33% (8 of 24) German doctors estimated less than 10% (close! -- 9%)
- 95% of American doctors estimated around 75% (far! -- 9%)