- You have a homework assignment due Friday. Questions?
- You have an assigned Reading for next time: Graphs
- We were investigating the Sierpinski's triangle, an area fractal.
- We re-visited Pascal's triangle, and saw how we could use a fractal property of the triangle to show that the sum of the rows is a power of 2.
- We found the Fibonacci numbers within Pascal's triangle.
- We also discovered Sierpinski's triangle within Pascal's triangle.
- The "Bridges of Konigsberg" problem started graph theory: "is it possible to set off and walk around Konigsberg crossing each bridge exactly once?" (p. 116 of your reading on graphs):
Try it yourself. Here is the problem abstracted:
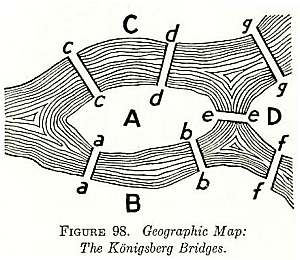
"It being customary among the townsmen, after some hours in the Gasthaus [on the island], to attempt to walk the bridges, many have returned for more refreshment claiming success. However, none have been able to repeat the feat by the light of day."
- Solved by Euler
(1735), the beginning of graph theory.
- Graphs are made up of vertices (points) and edges
that connect the vertices. More formally, a graph is
- A collection of points, called vertices.
- A collection of edges, each of which connects two vertices.
- The degree of a vertex is the number of edges coming into it.
- Graphs are made up of vertices (points) and edges
that connect the vertices. More formally, a graph is
- Euler's solution:
- Konigsberg: To be traversable, there must be at most two vertices of odd degree.
- Euler noticed the so-called "hand-shaking theorem": in any graph, the number of vertices with odd degree must be even.
- An alternative solution -- thanks to spiked math
- Solved by Euler
(1735), the beginning of graph theory.
- You've
probably been making graphs for a long time.... (the pentagram)
- Definition of a graph: a graph is
- a collection of vertices,
- a collection of edges, and
- a set of rules, one for each edge, telling how each edge is connected to its pair of vertices.
- Graphs don't change by bending edges, but breaking them or
detaching edges from their vertices (and hence creating new vertices)
gives new graphs.
- A graph is simple if it doesn't have any loops (edges connected
from a vertix to itself), or multiple edges with the same two vertices.
- Exercise: draw all the simple graphs with three vertices.
- A cycle is a route from a node back to itself that doesn't retrace steps.
- One of these graphs is a tree: a graph that has no cycles.
- Where have we seen trees used before?
- Exercise: you draw all the simple graphs with four vertices.
- Have you ever seen any of these before? Could we give any of them names?
- Planar graphs are graphs that can be drawn such that no two edges
intersect.
- Complete graphs are simply graphs with connections between
every pair of vertices (but no loops).
- Exercise: Let's see if we can show that the complete graph
with five vertices is not planar:
- We can show that the complete graph with four vertices is planar.
- Why isn't the five graph planar? What happens?
- The three utilities and three houses graph is not planar, either:
- Any non-planar graph has a copy of one of these two graphs
in it somewhere, as a subgraph:
