- You have a homework assignment due today, on fractals.
- You also had an assigned Reading for today: Graphs. I hope that you had a chance to read it.
- Review, emailed to me this morning: "NKU student opera this Friday at 8 pm and Sunday at 3 pm, Greaves. The opera is Dr. Miracle (Bizet). The students are doing a great job. It's very funny (and short -- under an hour). You'll enjoy the show!"
- You have two readings that concern graphs coming up from your text. It wouldn't hurt to do those ASAP.
- We started in Konigsberg, Prussia, with a game about bridges. Can we traverse all the bridges before traversing any one of them twice?
- We encountered the definition of a graph as a set of vertices (or points), some connected by edges.
- We discovered Euler's solution to this problem: traversal is possible only if there are either 0 or 2 odd-degreed vertices.
- Graphs don't change by bending edges, but breaking them or
detaching edges from their vertices (and hence creating new vertices)
gives new graphs.
- A graph is simple if it doesn't have any loops (edges connected
from a vertix to itself), or multiple edges with the same two vertices.
Now: how might we relate this concept to Facebook?
- Exercise: let's draw all the simple graphs with one, two,
and three vertices.
- A cycle is a route from a node back to itself that doesn't retrace steps.
- One of these graphs is a tree: a graph that has no cycles.
- Where have we seen trees used before?
- Exercise: you draw all the simple graphs with four vertices.
- Have you ever seen any of these before? Could we give any of them names?
- Planar graphs are graphs that can be drawn such that no two edges
intersect.
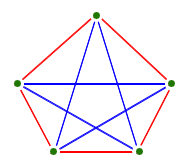
- Complete graphs are simply graphs with connections between
every pair of vertices (but no loops).
- Exercise: Let's see if we can show that the complete graph
with five vertices is not planar:
- We can show that the complete graph with four vertices is planar.
- Why isn't the five graph planar? What happens?
- The three utilities and three houses graph is not planar, either:
- Any non-planar graph has a copy of one of these two graphs
in it somewhere, as a subgraph:
