Day 29, Mat227

Last time

Next time

Announcements:
- Your 6.8 homework will be due Wednesday -- again, sorry to keep the pressure up, but we've got to keep moving....
- Your 6.6 homework is due today
section 6.8: L'Hopital's Rule (Sometimes limits are kind of tricky....)
- In financial mathematics we tend to use an unusual base for an exponential:
  
  ${P(t)=P_0\left(1+\frac{r}{n}\right)^{nt}}$
- You may have encountered a few laws such as The rule of 72 (70, 71, 69.3,...) to calculate doubling time: forget them! Just do the math: the question is
  
  For what value of t is ${P(t)={P_0\left(1+\frac{r}{n}\right)^{nt}}={2{P_0}}}$ ?
  
  Solving for t in ${P_0\left(1+\frac{r}{n}\right)^{nt}=2P_0}$ , we get
  ${t=\frac{\ln 2}{n\ln(1+\frac{r}{n})}}$
  
  where n is the number of compoundings per year, and r is given as a decimal (e.g. 9% is represented by .09). This is the doubling time.
  When compounding is continuous (i.e. ${n{\to}{\infty}}$ ), this reduces to the very lovely rule
  ${\frac{\ln 2}{r}}$
- Now, how do we know that ${\lim_{n \to \infty}\frac{\ln 2}{n\ln(1+\frac{r}{n})}=\frac{{\ln{2}}}{r}}$ ? That is, how do we know that
  
  ${\lim_{n \to \infty} \ {n\ln(1+\frac{r}{n})}={r}}$ ?
  The answer is provided by L'Hopital's Rule, which is useful in solving certain indeterminate limits:
  
  Let's rewrite it a little: we want to show that
  
  ${\lim_{n \to \infty}\frac{\ln(1+\frac{r}{n})}{{\frac{1}{n}}}={r}}$
- Here's the general situation:
- And if the limit of the quotient of the derivatives is indeterminate, then iterate -- that is, do it again! Then work with the ratio of the second (or higher) derivatives.
- Motivation of L'Hopital's Rule (requires the limit definition of the derivative -- p. 471) in the case where ${f(a)=0}$ and ${g(a)=0}$ .
  Consider ${\lim_{x\to{a}}\frac{f(x)}{g(x)}}$
- Examples:
  - Demonstration that ${\lim_{h \to 0} \frac{e^h-1}{h} = 1}$ (remember that this limit is just the limit definition of $f(x)=e^x$ ).
  - Let's do 9, 11, and 15 from p. 477
  - I asked my son Thad "What's ${0^0}$ ?" and he said "0." I tried to convince him that it should be 1 ("Any number to the 0th power is 1."). He tried to convince me that 0 to any power should be 0. His calculator said "undefined". Mathematica says "Indeterminate".
    
    What's ${\lim_{x\to{0}}{x^x}}$ ?
    (A trick with logs will help!)
  - #70, p. 478
  - #93, p. 479
Today we begin section 7.1: Integration by parts.
- First of all, the big picture: integration by parts is just the product rule backwards. This integration technique, like all integration techniques, is really just a differentiation technique in reverse.
  Consider the method of u-substitution, for example. That's just the chain rule in reverse.
- Derivation of the integration by parts formula:
  We start with the product rule:
  
  ${\left[u(x)v(x)\right]'=u(x)v'(x)+v(x)u'(x)}$
  Now integrate both sides:
  
  ${\int_{}^{}\left[u(x)v(x)\right]'dx=\int_{}^{}\left[{u(x)v'(x)+v(x)u'(x)}\right]dx}$
  
  ${\int_{}^{}u(x)v'(x)dx=u(x)v(x)-\int_{}^{}v(x)u'(x)dx}$
  
  ${\int_{}^{}udv=uv-\int_{}^{}vdu}$
- We'll motivate this technique by considering exercises #9 and #66, p. 492 in detail.
- Integration by parts may need to be carried out multiple times: sometimes the idea is to simplify the integral each time, until a really simple one arises allowing us to calculate the final solution (e.g. Example 6, p. 491). Sometimes it's something of a trick: we compute the integral multiple times in order to return to the original integral, allowing us to solve an equation for the original integral (e.g. Example 4, p. 490).
- Suggested strategy:
  - Choose u so that u' is simpler than u itself.
  - Choose v' so that $v=\int_{}^{}v'dx$ can be evaluated.
  - Sometimes v'=1 is a good choice.
- Of course, all this works with definite integrals:
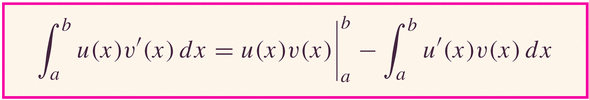
- Examples:
  1. #9, p. 492
  2. #10
  3. #26
  4. #39
  5. #40
  6. #51

Website maintained by Andy Long. Comments appreciated.