- Your 6.6 homework is returned: graded
- #9, p. 459
- #12
- #47
- I just have to share one story from my Peace Corps days:

No student has ever worked harder than Kpandja.
- First of all, the big picture: integration by parts is just the
product rule backwards. This integration technique, like all
integration techniques, is really just a differentiation technique in
reverse.
Consider the method of u-substitution, for example. That's just the chain rule in reverse.
- Derivation of the integration by parts formula:
We start with the product rule:
Now integrate both sides:
- We'll motivate this technique by considering an important example:
- Integration by parts may need to be carried out multiple times:
sometimes the idea is to simplify the integral each time, until a
really simple one arises allowing us to calculate the final solution
(e.g. Example 6, p. 491). Sometimes it's something of a trick: we
compute the integral multiple times in order to return to the original
integral, allowing us to solve an equation for the original integral
(e.g. Example 4, p. 490).
- Suggested strategy:
- Choose u so that u' is simpler than u itself.
- Choose v' so that
can be evaluated.
- Sometimes v'=1 is a good choice.
- Of course, all this works with definite integrals:
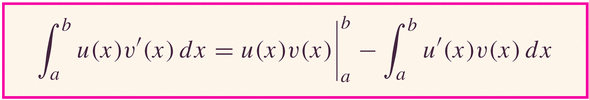
- Examples:
- #9, p. 492 (sometimes the function to integrate is 1!)
- #10 (ditto)
- #26
- #39
- #40
- #51
- #66,