Day 06 in Mat360

Last time:

Next time:

Today:

Announcements:
- Your third homework is due today.
- Your fourth homework is due next time, Tuesday 2/3, and your first programming assignment is due Thursday 2/5.
- A fifth homework will be due on the 10th of February (and note that I've moved some of assignment 4 to assignment 5, so that you have less to do for Tuesday).
Today we're going to finish off chapter 2 (one way or the other!). That means that we'll be starting into Chapter 3 next time: please read into it. We're going to be considering root-finding.
Section 2.2: Floating-Point Numbers

In this section the authors describe the manner in which numbers are stored in the computer. They focus on "floating-point numbers", which are represented by three parts:
1. The sign of the number
2. The position of the "radix" point (aka decimal point in base 10) -- we might say the "order of magnitude" of the base.
3. The mantissa (the known digits)
So a number is given in what looks like scientific notation, e.g. +2.99792458E08 (m/s) Question: What is that number?
Definition 2.1: A real number is said to be an n-digit number if it can be expressed as
${{\pm}10^e{\times}d_1.d_2\ldots{d_n}}$
Question: They then ask "What's an n-bit number?" (p. 39) What do you tell them?
Let's imagine that our machine has base-10 architecture, with ${-9\le{e}\le{9}}$ , and ${n=4}$ . Then we know exactly which numbers may be represented: numbers from

Largest magnitude numbers -9.999x10⁹ +9.999x10⁹

Smallest magnitude numbers -1.000x10^-9 +1.000x10^-9

You might think that we could consider smaller numbers (e.g. +0.001x10^-9), but our numbers are frequently normalized so that the leading digit () is non-zero (except for 0 itself). This gives us exactly the same number of digits at each order of magnitude of 10.
Failure to include the denormalized numbers (that don't have a leading 1) leads to a gap around zero in this figure:

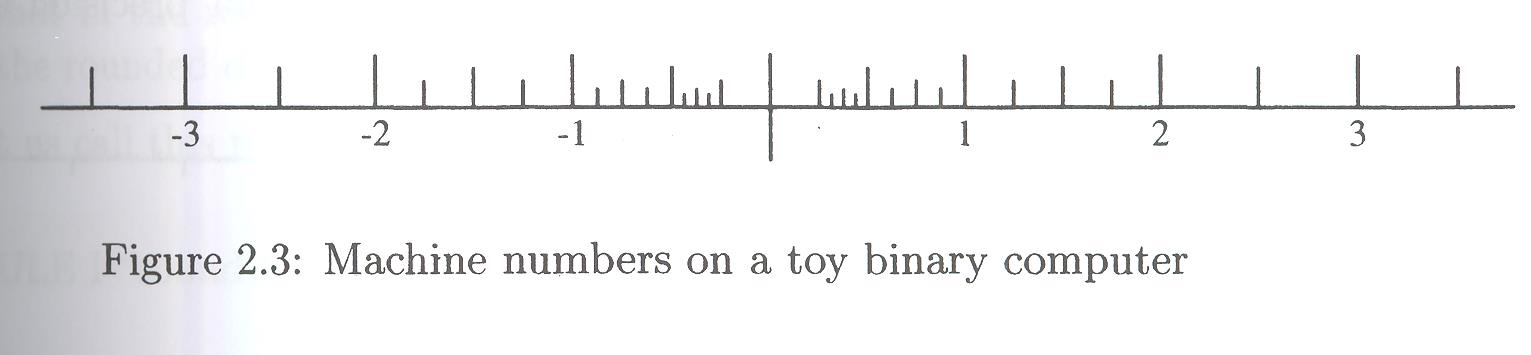
We see that the smallest positive number representable is 1/4. The smallest subdivision is 1/16. It seems that 4 may not be representable. What might be the toy machine representation architecture?
On the downside, if we allowed non-zero leading digits, then there would be redundant representations for many numbers (e.g. +1.000x10^-9=+0.100x10^-8)
Question: what do all the machine numbers look like if we restrict a binary machine so that it has architecture ${-2\le{e}\le{1}}$ , and ${n=3}$ ?
Now, in reality, computations are usually done in base 2, and the IEEE standard for single precision and double precision are

Single Double

Base 2 2

n 24 53

e [-126:127] [-1022:1023]

Question: in each case, how many exponents are there in the exponent range? Of what significance are these numbers (or numbers close, rather...)?
Question: let's see if we can make sense of this system with this particular example:
```
	;; 0  01111100   01000000000000000000000
	;; + power of 2   mantissa (significand)      
	;; 
	;; The first bit of the mantissa is an implied 1 (normalized form). 
	;; 
	;; Since the powers of 2 are all positive, we have to shift the exponent to get
	;; both positive and negative exponents. The IEEE standard is to subtract 127
	;; from the exponent.
	;; 
	 
	
```
Our authors describe the difference between precision and accuracy at this point: I think that it's best done graphically:
Section 2.3: Rounding

"The purpose of rounding in computation is to turn any real number into a machine number, preferably the nearest one." (p. 43)
But there are different ways to do it. You're no doubt familiar with rounding (but how do you handle ties -- that is, how do we round 19.5 to an integer?). The authors suggest several strategies (p. 43):
1. Rule 1: "round-to-even": if the digits following the nth digit are
  - less than 500000....
    then discard these digits
  - greater than 500000....
    then discard these digits and add 1 to the nth digit
  - exactly equal to 500000....
    then discard these digits and add 1 to the nth digit if it is odd.
  "Round-to-even" because if nth digit is even, do nothing; add 1 if odd, making it even. All nth digits become even.
2. Rule 2: "round-to-nearest, with round away from zero in case of a tie"
  Same as Rule 1, except when exactly equal to 500000....
  then round UP (away from zero).
  Inferior to Rule 1, as ever-so-slightly biased away from zero.
3. Rule 3: chopping -- "round-to-zero" -- truncation.
  Whatever comes after nth, just drop it.
  Inferior to Rule 1, as slightly biased toward zero.
The biases are illustrated nicely in Figure 2.5, p. 45:

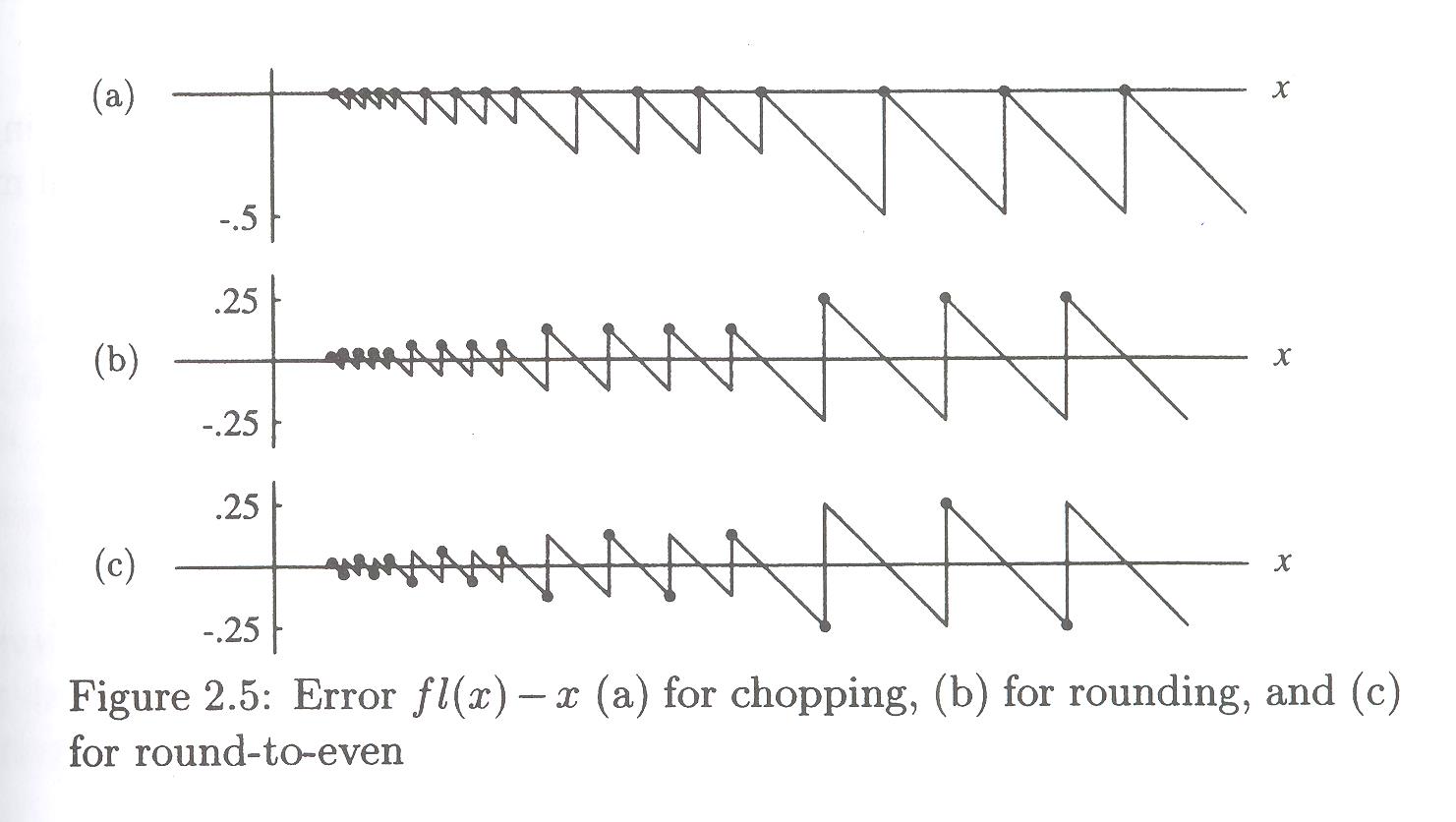
The chopping approximations are all under-estimates; the rounding methods give more balanced overs and unders; but the rounding alone has a bias for giving overestimates, which rounding-to-even balances out.
There is some vocabulary here with which we should be familiar: sometimes rounding results in
- overflow ( ${\pm{\infty}}$ )
- underflow (below the smallest possible machine number)
- NaN (not a number)
Definitions:

fl (float)
converts real numbers into machine numbers

A real number is said to be representable if
it rounds to a machine number (neither overflow nor underflow, nor NaN).

relative representation error:
${\frac{fl(x)-x}{x}\equiv{\delta}}$

The authors make the case that
${{\delta}\le\frac{1}{2}\beta^{1-n}{\equiv}unit\ rounding\ error}$ (tiny!)
where
- $\beta$ is the base, and
- ${n}$ is the precision (number of decimals in the mantissa)
Examples:
- But tiny things can have big consequences:
Section 2.4: Basic Operations

By "basic operations" the authors mean using standard arithmetic operations on machine numbers to produce machine numbers. There will be errors.
Let a and b be machine numbers, and let $\circ$ represent any of the standard arithmetic operations. Then

${a{\hat{\circ}}b{\equiv}{fl({a}\circ{b})}}$
I.e., to compute one of these binary operations with machine numbers, you do the operation exactly, and then convert it to a machine number with float (fl). We already know what this will cost: we'll have a roundoff error of $\delta$ .
As we compute more complicated function, however, with one unary or binary operation after another, the errors continue to accumulate (as seen for example, in section 2.4.5, p. 54).
Examples:
- #1, p. 54: Assuming four digit floating-point arithmetic with round-to-even rounding, perform the following computations:
  
  (a) 0.6668+0.3334 (b) 1000.-0.05001
  
  (c) 2.000*0.6667 (d) 25.00/16.00
- #9, p. 56
Section 2.5: Numerical Instability

This section features several interesting examples of functions, some of them tremendously important, which are also extraordinarily sensitive to errors.
The authors define numerical instability as "unacceptably large amplification of computational errors in an algorithm."
One of the main points of the section is that a "solution" to a problem may be technically correct, analytically correct, and yet poorly designed to produce good results in general.
Let's go through the example problem on pages 62-63. It's a simple calculation, but illustrates how the reasonable can go awry (answer is .00082713 to one more digit).
An excellent example is the quadratic formula. Many of you have memorized it as

${\frac{-b\pm\sqrt{b^2-4ac}}{2a}}$
We can imagine situations, however, for which this calculation may be dangerous. What do you notice?
Question: an old trick from your past may be used to improve things: can you think of how to change this formula, to make it less sensitive?
What about that difference inside the square root? The authors assert that "cancellation inside the radical is not easily avoided" (p. 65), and yet just below that remark they note that

${{x^2-y^2}{\Longrightarrow}{(x-y)(x+y)}}$
is better conditioned when ${x{\approx}y}$ . So what COULD we do (if we wished....)?
Examples:
- #6, p. 68

Website maintained by Andy Long. Comments appreciated.

The conjugate

They are represented in Figure 2.3.

how many base-10 digits of accuracy you have to the left of the decimal point.

An interval approximation for e: ${e{\in}[2.71828182{,2.71828183}]}$

One that showed 0, 1, or 2 for positions; we don't see a "2" here.

The figure illustrates two cases which won't work -- 1.44 and 1.45 -- each producing an interval beyond what the data support (the top line).

If not, and we must use 1.4, then another user would assume that we only know the 4 in the tenths place to within five units, and you can see what happens to the actual uncertainty -- it expands grossly, to the interval (0.9,1.9).

The speed of light in a vacuum.

When

${|a+b|<<|a|}$ ,

and, in particular, when ${a+b{\approx}{0}}$ , i.e. when

${a{\approx}{-b}}$ .

Symmetrically, subtraction will suffer the problem when a and b are approximately equal.