Day 9, Mat128: Calculus A

While you are always encouraged to ask questions in class, it might be particularly useful to do so on Wednesday! While we will not have a formal review for the exam, you may ask any questions you want to start.

• #16 -- There are infinitely many functions that make these conditions true.
• #20 -- you were to calculate the function for all those $x$-values given in the text. Show your work!
• #24 -- You were to use a table, according to the directions....

• You need to know the vocabulary of math, and the basic skills of algebra:
  1. tangent and secant lines
  2. slope of a line
  3. roots (places where $f(x)=0$)
  4. point-slope form of a line (only 7 of 28 -- 1/4 -- could write the equation of a linear function $f(x)$ that passes through two points, in point-slope form).

• Basic rules:
  • Constant rule:

  • Identity rule:

• General laws: Suppose that $\lim_{x \to a} f(x)$ and $\lim_{x \to a} g(x)$ exist. Then \[ \lim_{x \to a} [f(x)+g(x)] = \lim_{x \to a} f(x) + \lim_{x \to a} g(x) \] \[ \lim_{x \to a} [f(x)-g(x)] = \lim_{x \to a} f(x) - \lim_{x \to a} g(x) \] \[ \lim_{x \to a} [cf(x)] = c\lim_{x \to a} f(x) \] \[ \lim_{x \to a} [f(x)g(x)] = \lim_{x \to a} f(x) \lim_{x \to a} g(x) \] \[ \lim_{x \to a} \frac{f(x)}{g(x)} = \frac{\lim_{x \to a} f(x)}{\lim_{x \to a} g(x)} {\text{ if }} \lim_{x \to a} g(x) \ne 0 \]

• As discussed last time, we can proceed to deduce that all polynomials have limits, and furthermore that

  \[ \lim_{x\rightarrow{a}}P(x)=P(a) \]

  Last time we looked at a simple example of the "polynomial rule": We used limit laws to show that it works for $P(x)=9x^3-6x^2+x-7$.

  Now we know why it is nice to have a "polynomial law" -- so that we don't have to go through that every time.

• Other Laws:
  • The squeeze theorem What can we say about the limit of g as x approaches a?

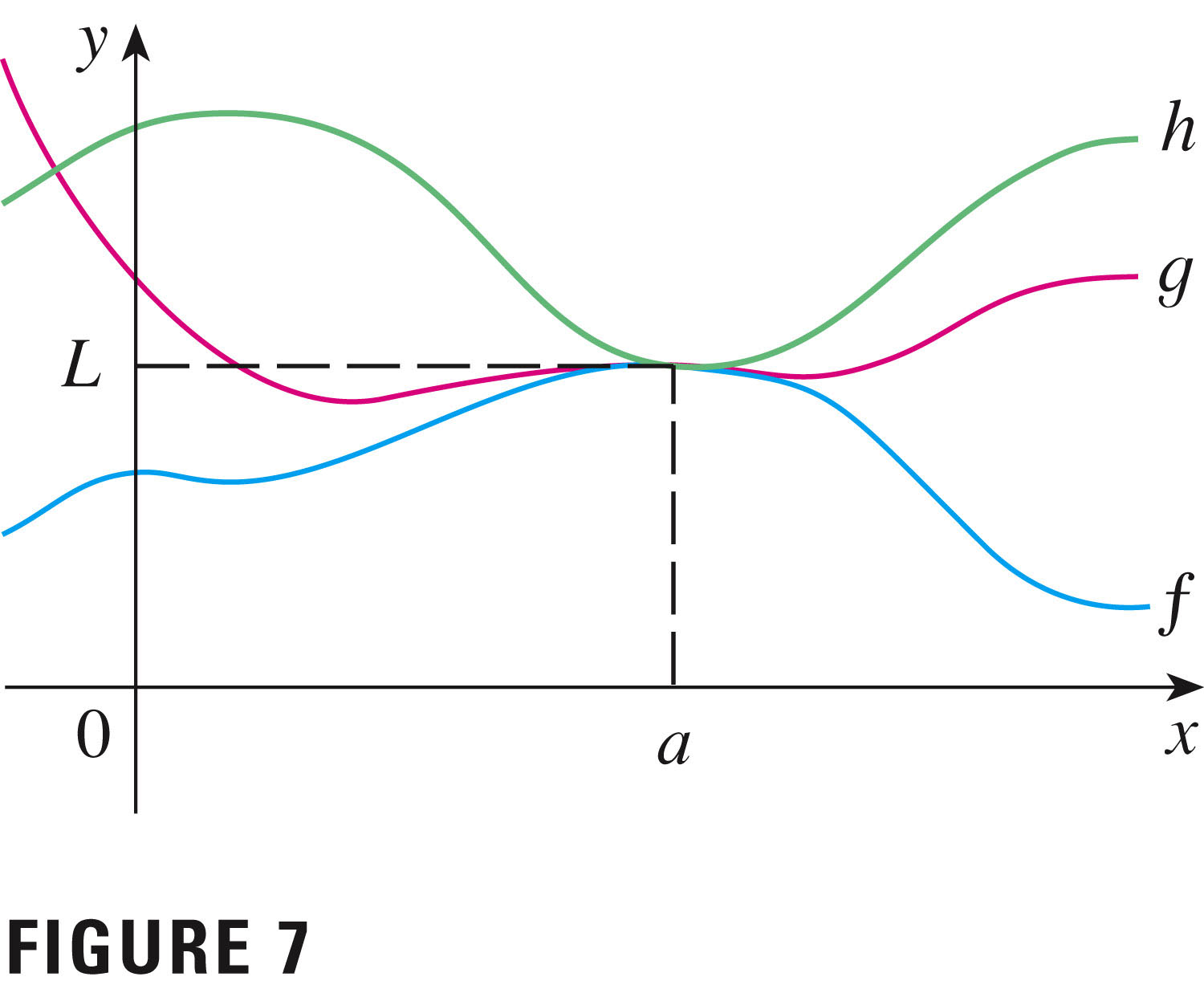
  Before we jump back to some more examples, let me remind you of why we are concerned especially about the quotient law (and its restriction that the denominator must not have zero as a limit): Example 5, p. 66.

  This is an example of a derivative calculation: we can think of this as $f'(a)$, where $f(x)=x^2$ and $a=3$. Let's see. Recall that

  $f'(a)=\lim_{h\to 0}{\frac{f(a+h)-f(a)}{h}}$

• Some Examples.

  Keep your eye on some of the "tricks" we use to turn ugly indeterminate expressions into equivalent expressions for which we can evaluate the limits.

  These tend to be tricks of algebra.

  • Example 3, p. 65
  • #7, p. 69
  • #10
  • #25
  • #33
  • #47
  • #54

• Additional examples:
  • #63, p. 71
  • #59, p. 71 (squeeze it!)

• A new administration in government?
• A sidewalk?
• Coffee poured into a cup?

Note: three things have to happen:

1. The limit of $f$ exists at $a$,
2. The function value $f(a)$ exists at $a$, and
3. The two values are equal.

Otherwise is discontinuous at

There are various kinds of discontinuity (which we've already seen):

• Removable discontinuities (e.g. holes)
• Jump discontinuities
• Infinite discontinuities

This function has a limit at zero (-.5), but is not defined there.

• We define one-sided continuity
• we have sum laws, product, and quotient laws. We've already used these to demonstrate that polynomials are continuous on all real numbers:
  

• Polynomials
• Rational functions: (ratios of polynomials)
• Trigonometric functions: sine, cosine, tangent
• Root functions: $f(x)=x^{1/n}$
• Exponential functions: $f(x)=b^x$

• Roughly: A composition of continuous functions is continuous.

• Let $F(x)=f(g(x))$ be a composite function.

  If $g$ is continous at $x=c$ and $f$ is continous at $g(c)$ then

  $F(x)$ is continuous at .

• Theorem: Suppose that f is continuous on the closed interval [a,b] and let N be any number between f(a) and f(b), where $f(a)\ne{f(b)}$. Then there exists a number $c$ in $(a,b)$ such that $f(c)=N$.

• Example: pp. 93, #69