- Today we have our first major/minor lunch:

Get yours before class!
- Your assignment for section 1.5 is due today.
- Your assignment for section 1.6 is due Monday.
- We have our first exam next Friday.
- Your 1.4 homework is returned: 2 and 7 graded.
- Answer the question. "What conclusions can you draw?"
- Show work.
- Give units.
- Limit laws:
- Basic rules:
- Constant rule:
- Identity rule:
- Constant rule:
- Sum law: "the limit of a sum is the sum of the limits"
So we use the basic laws above, and this "limit law", to conclude that
\[ \lim_{x\to{a}}(x+c)=a+c \]
- The Difference law, product law, quotient law (slight caveat here
-- no zero denominators), power law, and root law work about the same
way (remember the domain restriction for roots -- that is, fractional
powers).
- As discussed last time, we can proceed to deduce that all
polynomials have limits, and furthermore that
\[ \lim_{x\rightarrow{a}}P(x)=P(a) \]
Let's look at a simple example of the "polynomial rule": how can we show that it works for, say, $P(x)=9x^3-6x^2+x-7$?
This is why it is nice to have a "polynomial law" -- so that we don't have to go through this every time.
- Other Laws:
- The squeeze theorem
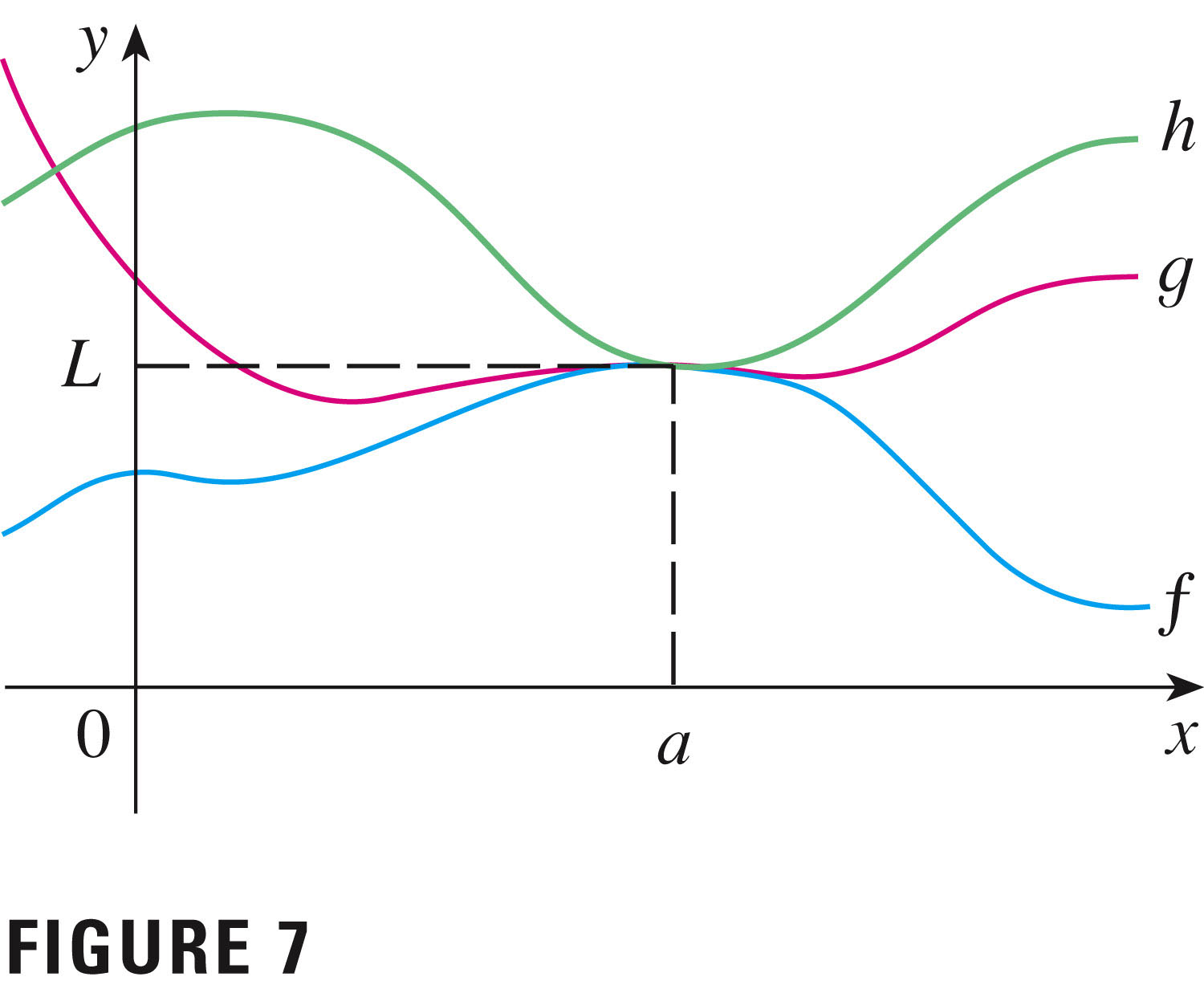
- The squeeze theorem
- Now let's take a look at some of the examples from the section
exercises.
Keep your eye on some of the "tricks" we use to turn ugly indeterminate expressions into equivalent expressions for which we can evaluate the limits.
- Example 3, p. 65
- #7, p. 69
- #10
- #25
- #33
- #47
- #54
- Additional examples:
- #63, p. 71
- #59, p. 71 (squeeze it!)
- Basic rules: