- This Friday we have our first major/minor lunch:

- Your quizzes are returned, as is your first homework.
- quizzes:
- "Justify" means "Explain". Without justification, you'll get few points....
- You need to label graphs.
- homework:
- Use "zoom and line fit" means that I should see some zoomin' and some fittin'!:)
- Adel did it in Mathematica. So did Weston, and several others. Good!
- Justin has a nice version on paper....
- quizzes:
- Generally each problem is graded out of two, so your
assignment is out of 4.
- You have an assignment due today.
- You have an assignment due for next time. Keep up!
- Limit laws:
- We start with two especially trivial special limits:
- Constant rule $(f(x)=c)$:
Here the function $f(x)=1$ is plotted. As $x \to 0$, the $y$-values head to 1. Well, more to the point, they never vary from 1! Quite a boring function....
- Identity rule $(f(x)=x)$:
Here the function $f(x)=x$ is plotted. As $x \to 0$, the $y$-values head to 0. And the closer $x$ gets to 0, the closer $y$ gets to 0. That's the way it's supposed to work! Also a rather boring function: so predictable!
What can we do with those? We need more horsepower....
- Constant rule $(f(x)=c)$:
- Sum law: "the limit of a sum is the sum of the limits"
So what is this limit:
This sum (and many other operations) satisfy the same pattern:
"The limit of a STUFF is the STUFF of the limits." So, in particular,
"The limit of a sum is the sum of the limits." - Difference law
- Product law
- Constant multiple law
- Quotient law (slight caveat here -- no zero denominators)
- Power law
- Root law -- again, a caveat: why can't we compute
\[ \lim_{x\to{0}}\sqrt{x} \]
Because the function isn't even defined as x approaches 0 from the left (square roots of negative numbers are imaginary). So we have only a one-sided limit, that \[ \lim_{x\to{0^+}}\sqrt{x}=0 \] Of course we can say that \[ \lim_{x\to{1}}\sqrt{x}=1 \] Limits exists everywhere else on the domain of the sqrt function. - Putting these laws together
- Now that we've got the sum and product and constant multiple rules, what can we deduce?
- "Affine" rule, for one:
\[ \lim_{x\to{a}}(mx+b)=ma+b \] - Then we can proceed to deduce that all polynomials have limits, and
furthermore that
This is the conclusion of Exercise #55, p. 71, which says that polynomials are continuous, which we'll consider more in section 1.8.
Exercise #56 says it's also true for rational functions, for every element of their domain.
- Take a look at a couple of the examples in the text, examples 5
and 6 on page 66. These both illustrate the limiting
process applied to the most
important definition in calculus:
$f'(x)=\lim_{h\rightarrow{0}}{\frac{f(x+h)-f(x)}{h}}$ In this case, both show examples of a slightly different version of this most important definition, the derivative at a point $x=a$:
$f'(a)=\lim_{h\to 0}{\frac{f(a+h)-f(a)}{h}}$ - Other Laws
- The squeeze theorem
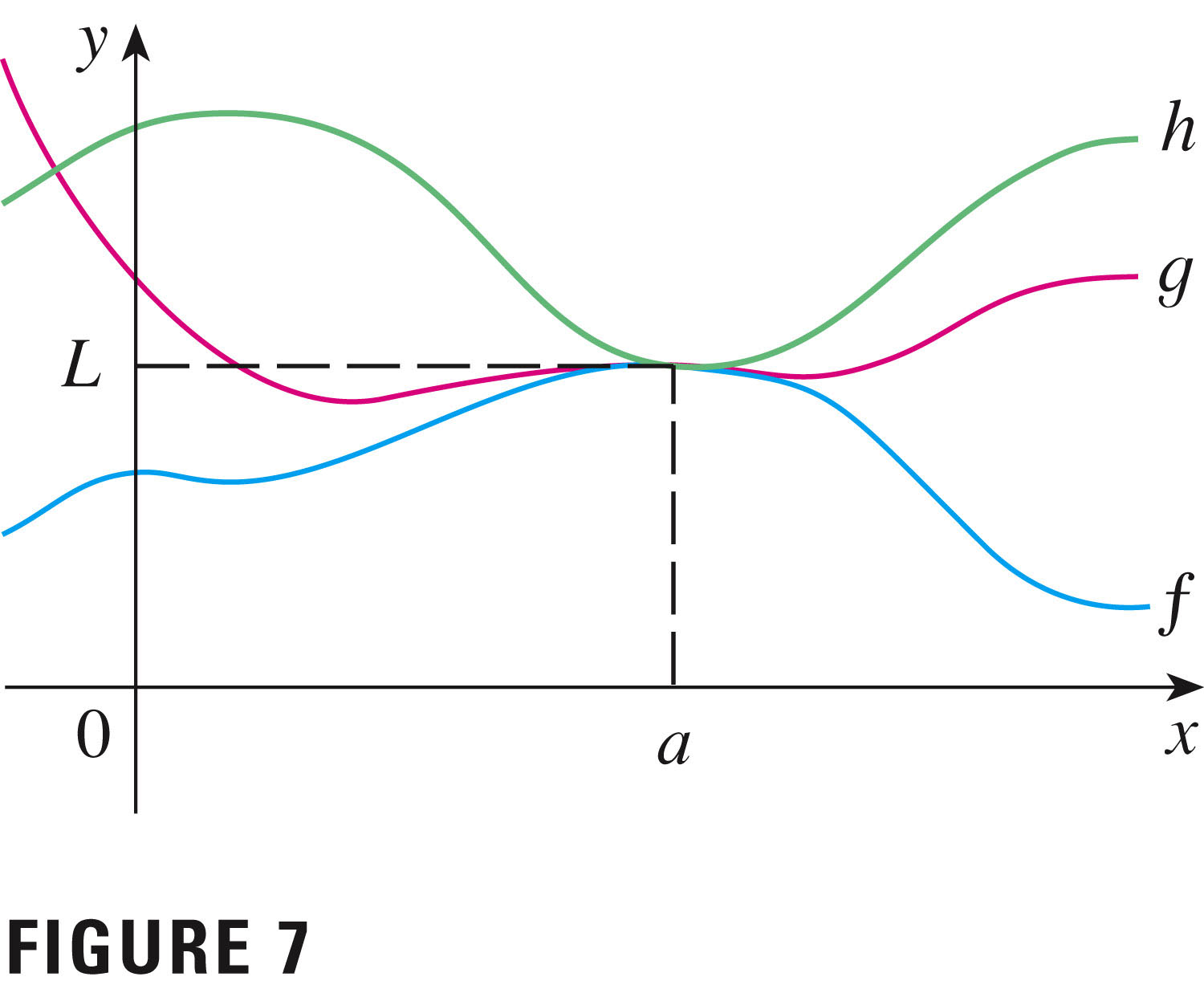
What's happening to the $y$-values?
- The squeeze theorem
- Now let's take a look at some of the examples from the section
exercises.
- Example 3, p. 65
- #7, p. 69
- #10
- #25
- #33
- #47
- #54
- Additional examples:
- #63, p. 71
- #59, p. 71 (squeeze it!)
- We start with two especially trivial special limits: