Day 6, Mat128: Calculus A

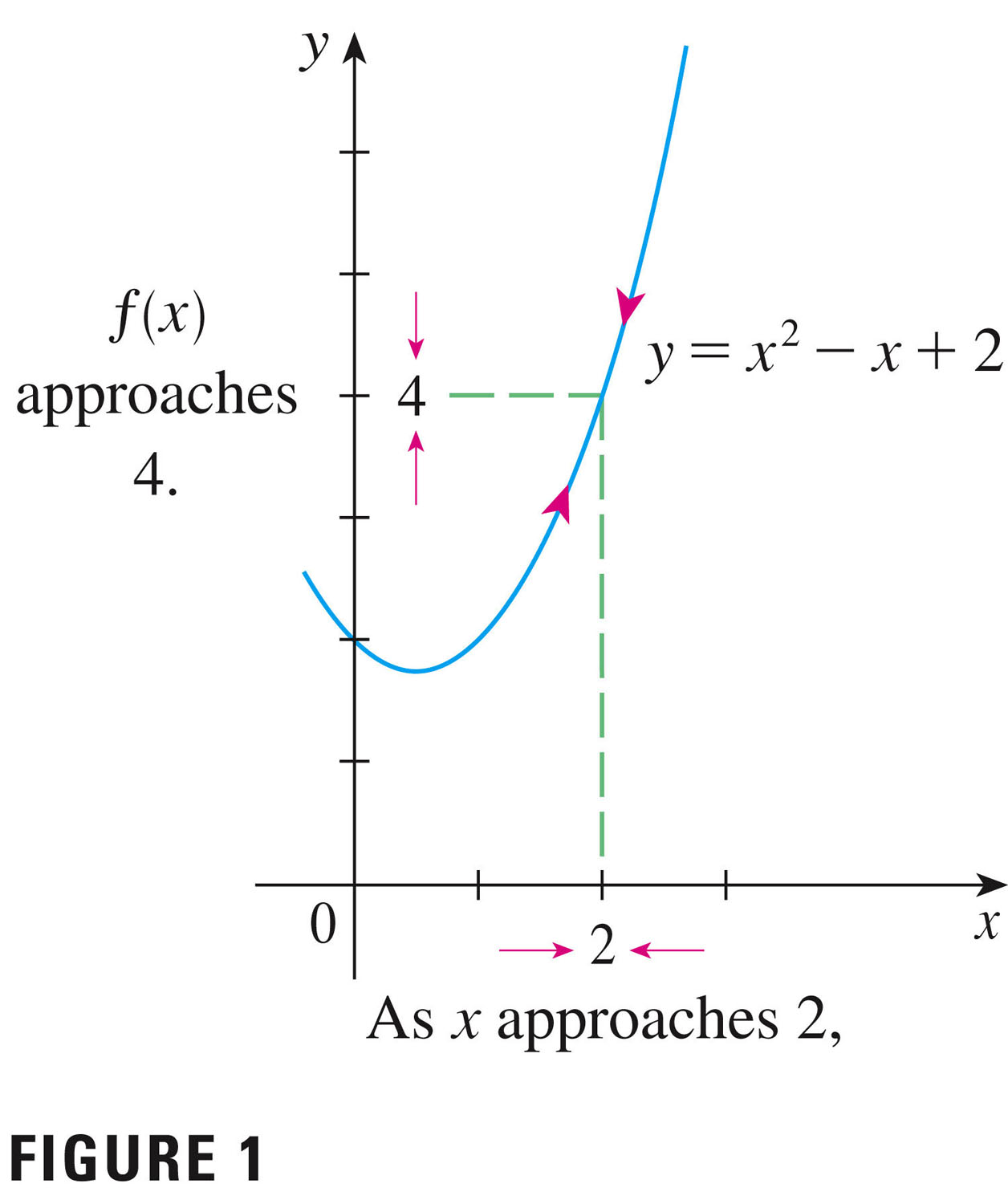
limit of $f(x)$ as $x$ approaches $a$: Suppose function $f(x)$ is defined when $x$ is near the number $a$ (this means that $f$ is defined on some open interval that contains $a$, except possibly at $a$ itself.) Then we write \[ \lim_{x \to a}f(x) = L \] if we can make the values of $f(x)$ arbitrarily close to $L$ by taking $x$ to be sufficiently close to $a$ but not equal to $a$. We say that "the limit of $f(x)$ as $x$ approaches $a$ equals $L$." The intuitive idea is that in the neighborhood of $a$, the function $f$ takes on values close to $L$.

We can approach $x=a$ from the left or from the right. We define limits from the left and from the right, and then say that the limit exists as $x$ approaches $a$ if and only if the limits from the left and right exist, and agree: if \[ \lim_{x \to a^-}f(x) = L \] and \[ \lim_{x \to a^+}f(x) = L \] then \[ \lim_{x \to a}f(x) = L \]

Last time we checked out some examples from section 1.5 -- not only the limits, but also what dangers lurk, even when we have very good technology. You can't always trust your calculator; trust your brain first.

• Let's check the last of the examples from section 1.5, to get started. One more lie....

  So limits may be infinite (one-sided, perhaps). Here's how we define that:

  infinite limits for $\displaystyle f(x)$ as $\displaystyle x$ approaches $\displaystyle a$: \[ \lim_{x \to a}f(x) = \infty \] means that the values of $\displaystyle f(x)$ can be made arbitrarily large (as large as we please) by taking $\displaystyle x$ sufficiently close to $\displaystyle a$ (but not equal to $\displaystyle a$). Similarly we can define \[ \lim_{x \to a}f(x) = -\infty \] and one-sided limits such as \[ \lim_{x \to a^-}f(x) = \infty {\hspace{1.5in}} \lim_{x \to a^+}f(x) = \infty \]

  

  In any of these cases, we define a vertical asymptote of the curve $\displaystyle y=f(x)$ at $\displaystyle x=a$.

• #18, p. 60
• #26, p. 60
• #35, p. 61
• #42, p. 61