Day 5, Mat128: Calculus A

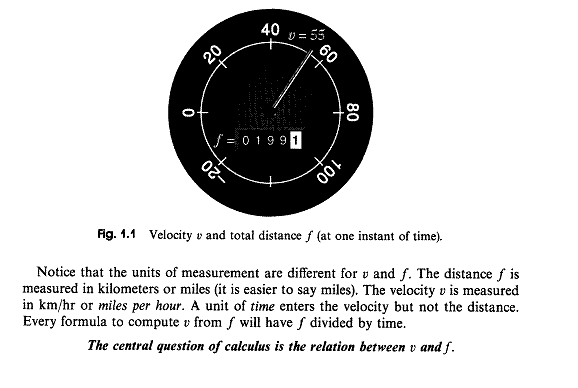
The velocity part is the derivative; the total distance part is the integral. In this course, we're focused on derivatives, hence the velocity. In particular, we speak of "instantaneous velocity" -- the velocity at a single point in time.

That's what your speedometer is showing (or attempting to show -- in reality it shows an average rage of change, the average velocity over a very short period of time).

It doesn't mean that you shouldn't read the text, however!

So hopefully you've already read section 1.5, and you're up to speed with notation.

The most important definition in calculus is the derivative (here is the derivative of $f$ at $x$):

And that's why we're so concerned about limits! Memorize it. Be able to write it at a moment's notice.

We've seen this in another form already:

This was defined as the slope of the tangent line to a curve (provided the tangent line exists).

Some Review points:

• Function representation
• Variables -- independent and dependent. [In the first limit above, the independent variable is actually $h$ for a fixed value of $x$.]
• Domains and Ranges
• Function composition
• Ratios!
• Indeterminate things... (division by 0)

We've seen how the secant lines approach the tangent line for a smooth curve. It's one of the first important problems we'll want to address in calculus. It's why we're interested in limits of things at the outset.

We usually find the equation of a line using two points, or a point and a slope. The secant line method approaches the tangent lin at a point by using a succession of nearby points that are ever closer to the point of tangency.

The tangent ("touching") line osculates ("kisses") the curve at this point.

Notice the focus on linear functions: linear functions are the most important functions in calculus.

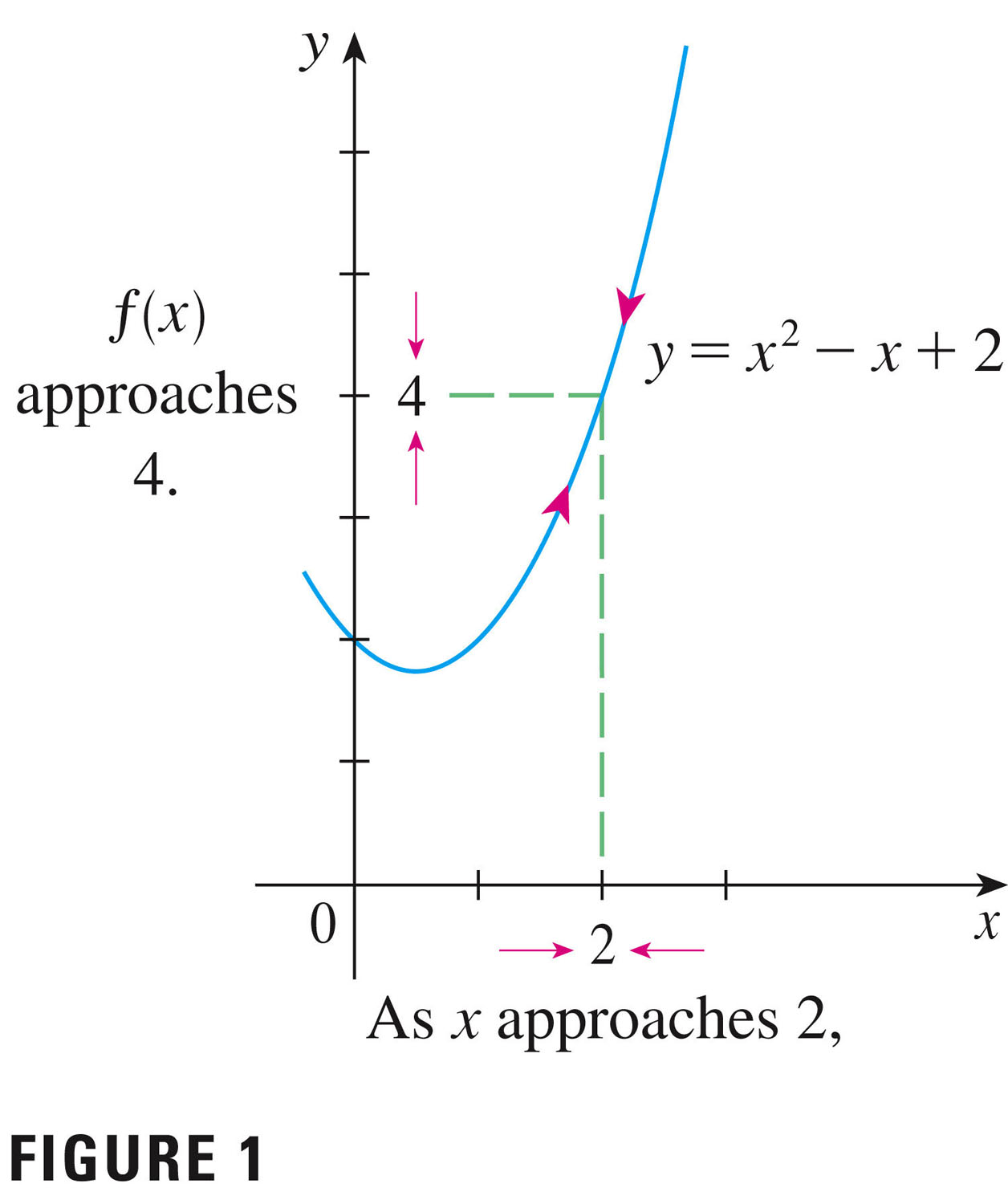
limit of $f(x)$ as $x$ approaches $a$: Suppose function $f(x)$ is defined when $x$ is near the number $a$ (this means that $f$ is defined on some open interval that contains $a$, except possibly at $a$ itself.) Then we write \[ \lim_{x \to a}f(x) = L \] if we can make the values of $f(x)$ arbitrarily close to $L$ by taking $x$ to be sufficiently close to $a$ but not equal to $a$. We say that ``the limit of $f(x)$ as $x$ approaches $a$ equals $L$.'' The intuitive idea is that in the neighborhood of $a$, the function $f$ takes on values close to $L$.

Questions:

• In the figure what is $a$, and what is $L$?
• To what class of functions does $f$ belong?
• Do limits (i.e. do we) even care about what happens exactly at $a$?

We can approach $x=a$ from the left or from the right. We define limits from the left and from the right, and then say that the limit exists as $x$ approaches $a$ if and only if the limits from the left and right exist, and agree: if \[ \lim_{x \to a^-}f(x) = L \] and \[ \lim_{x \to a^+}f(x) = L \] then \[ \lim_{x \to a}f(x) = L \]

You try: Consider $f(x)=\sin(x)$. Try finding the slope of the tangent line when $x=2$, and check with your neighbor. Draw the graph of $f(x)$, and add in the tangent line.

Let's check out some Mathematica examples from section 1.5, and check out not only the limits, but also what dangers lurk, even when we have very good technology. You can't always trust your calculator; trust your brain first.

We'll be using Mathematica extensively in this class. Have I told you that you have the right to a free copy of Mathematica?

Let's take a look at a few problems from the text (pp. 59--).

• Let's check the last of the examples from section 1.5, to get started. Mathematica tells one more lie!

  So limits may be infinite (one-sided, perhaps). Here's how we define that:

  infinite limits for $\displaystyle f(x)$ as $\displaystyle x$ approaches $\displaystyle a$: \[ \lim_{x \to a}f(x) = \infty \] means that the values of $\displaystyle f(x)$ can be made arbitrarily large (as large as we please) by taking $\displaystyle x$ sufficiently close to $\displaystyle a$ (but not equal to $\displaystyle a$). Similarly we can define \[ \lim_{x \to a}f(x) = -\infty \] and one-sided limits such as \[ \lim_{x \to a^-}f(x) = \infty {\hspace{1.5in}} \lim_{x \to a^+}f(x) = \infty \]

  

  In any of these cases, we define a vertical asymptote of the curve $\displaystyle y=f(x)$ at $\displaystyle x=a$.

• #18, p. 60 -- be creative!
• #26, p. 60
• #35, p. 61
• #42, p. 61 -- one more dirty rotten lie!

  Note the symmetry, which allows us to check only one side.

  Symmetry is a very important (and under-discussed) aspect of mathematics. Keep an eye on even and odd functions.