Day 13, Mat128: Calculus A

• What is the difference between continuous and discontinuous things?
  • A new administration in government?
  • A sidewalk?
  • Coffee poured into a cup?
  • Arctic Sea Ice Anomalies:
    

• Definition: continuity at the point $x=a$: \[ \lim_{x\rightarrow{a}}f(x)=f(a) \]

  Note: three things have to happen:

  1. The limit of $f$ exists at $a$,
  2. The function value $f(a)$ exists at $a$, and
  3. The two values are equal.

  Otherwise $f$ is discontinuous at $a$.

  There are various kinds of discontinuity (which we've already seen):

  • Removable discontinuities (e.g. holes)
  • Jump discontinuities
  • Infinite discontinuities
  • Crazy discontinuities like the function we discussed last time, which was $x^2$ for rational values of $x$, and 0 for irrational ones.

• Maybe a better definition:
  A function is continuous on an interval if its graph can be traced there without lifting the pencil from the paper. (Try one! Make one smooth, and one really "jaggy".)

• Many of the functions we've considered so far satisfy this, although not all do: consider the "holy function"

  This function has a limit at zero (-.5), but is not defined there. If $f$ is not defined at $x=0$, then it cannot be continuous there. We can fix this, by the way.... Just define $f(0)$ to be the limit (the closed dot in the graph above).

• Since continuity is wrapped up with limits, we have the same kinds of results that we did in relation to limits:
  • We define one-sided continuity
  • we have sum laws, product, and quotient laws. We've already used these to demonstrate that polynomials are continuous on all real numbers:
    

• Classes of functions that are continuous on their domains:
  • Polynomials
  • Rational functions: (ratios of polynomials)
  • Trigonometric functions: sine, cosine, tangent
  • Root functions: $f(x)=x^{1/n}$
  • Exponential functions: $f(x)=b^x$

• For all these functions one can evaluate limits using the so-called "substitution method": simply plug in $a$ for $x$.

• An important theorem (p. 88), RE composite functions (remember that I told you how important compositions are? here's one place they show up....):
  • Roughly: A composition of continuous functions is continuous.

  • Let $F(x)=f(g(x))$ be a composite function.

    If $g$ is continous at $x=c$ and $f$ is continous at $g(c)$ then

    $F(x)$ is continuous at $x=c$.

• Examples:
  • pp. 90-93, #3, 10, 12, 19, 23, 36, 46 (with Mathematica)
  • That crazy function which was $x^2$ for rational values of $x$, and 0 for irrational ones, has an interesting property: it is continuous at only a single point! It satisfies the definition only at $x=0$: it's discontinuous everywhere else! That's pretty weird.

• The Intermediate Value Theorem is an important result of continuity:
  • Theorem: Suppose that f is continuous on the closed interval [a,b] and let N be any number between f(a) and f(b), where $f(a)\ne{f(b)}$. Then there exists a number $c$ in $(a,b)$ such that $f(c)=N$.

  • Example: pp. 93, #69

These are tangent lines (places where a line osculates a curve):

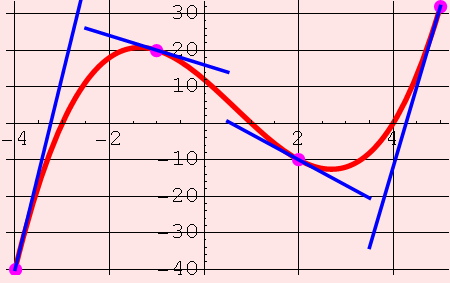
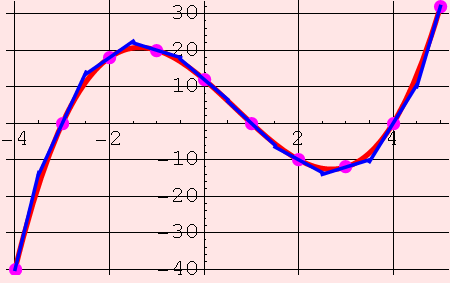
These are "rates of change" of the function f. What does that mean? The thing that tells you how fast a function is changing is its slope, isn't it? If a function is constant, then it's not changing at all. If the slope is steep (either up or down), then the function's values are changing dramatically and quickly.

The rate of change is dictated by the slope. So it should come as no surprise that the derivative of a function at a point is the same as the slope of the tangent line at a point:

We can approximate tangent lines with secant lines:

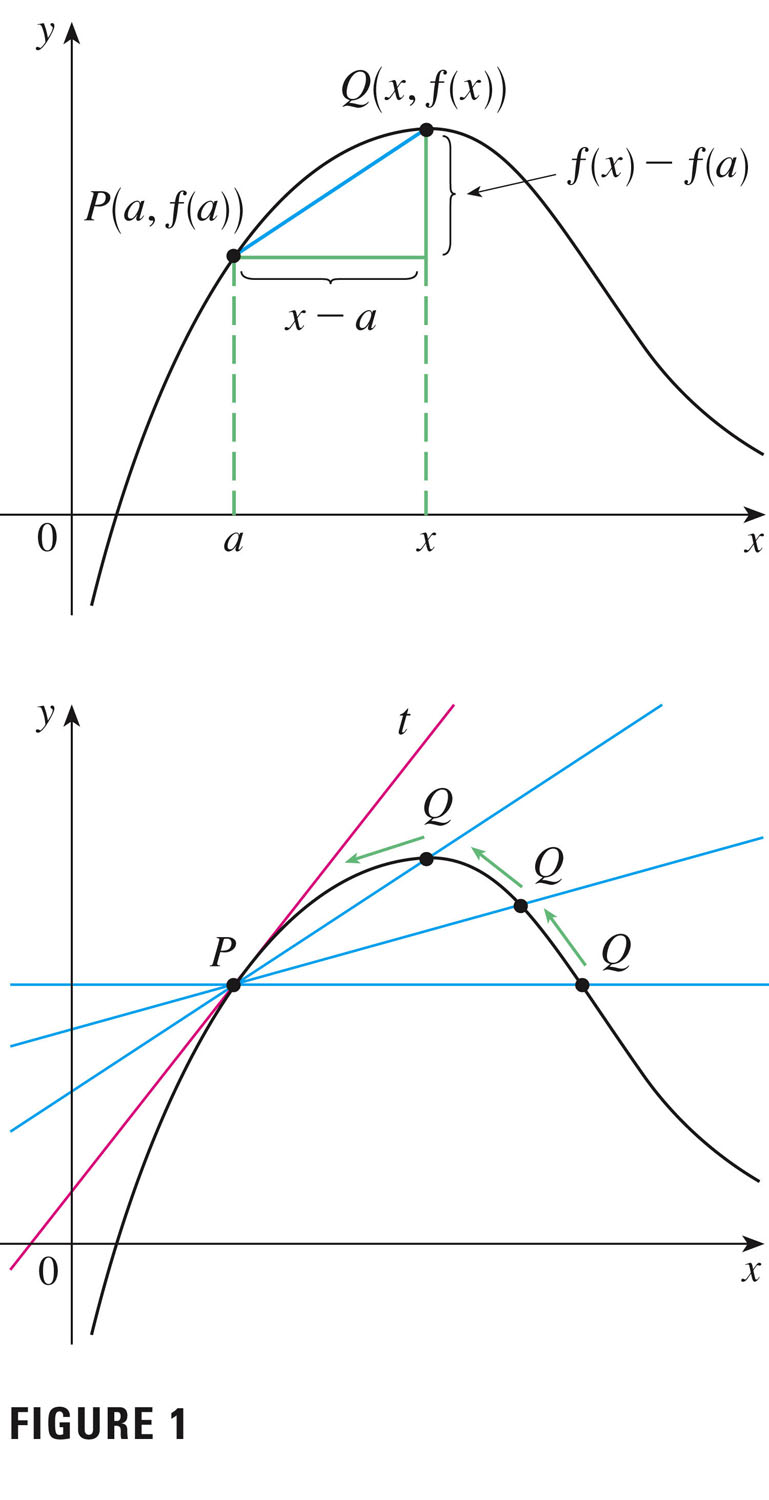
The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment (the slope of a secant line), $\frac{f(x)-f(a)}{x-a}$ This is an average rate of change in f over a finite interval. In the limit, this average rate of change becomes an instantaneous rate of change: $m=\lim_{x\to{a}}\frac{f(x)-f(a)}{x-a}$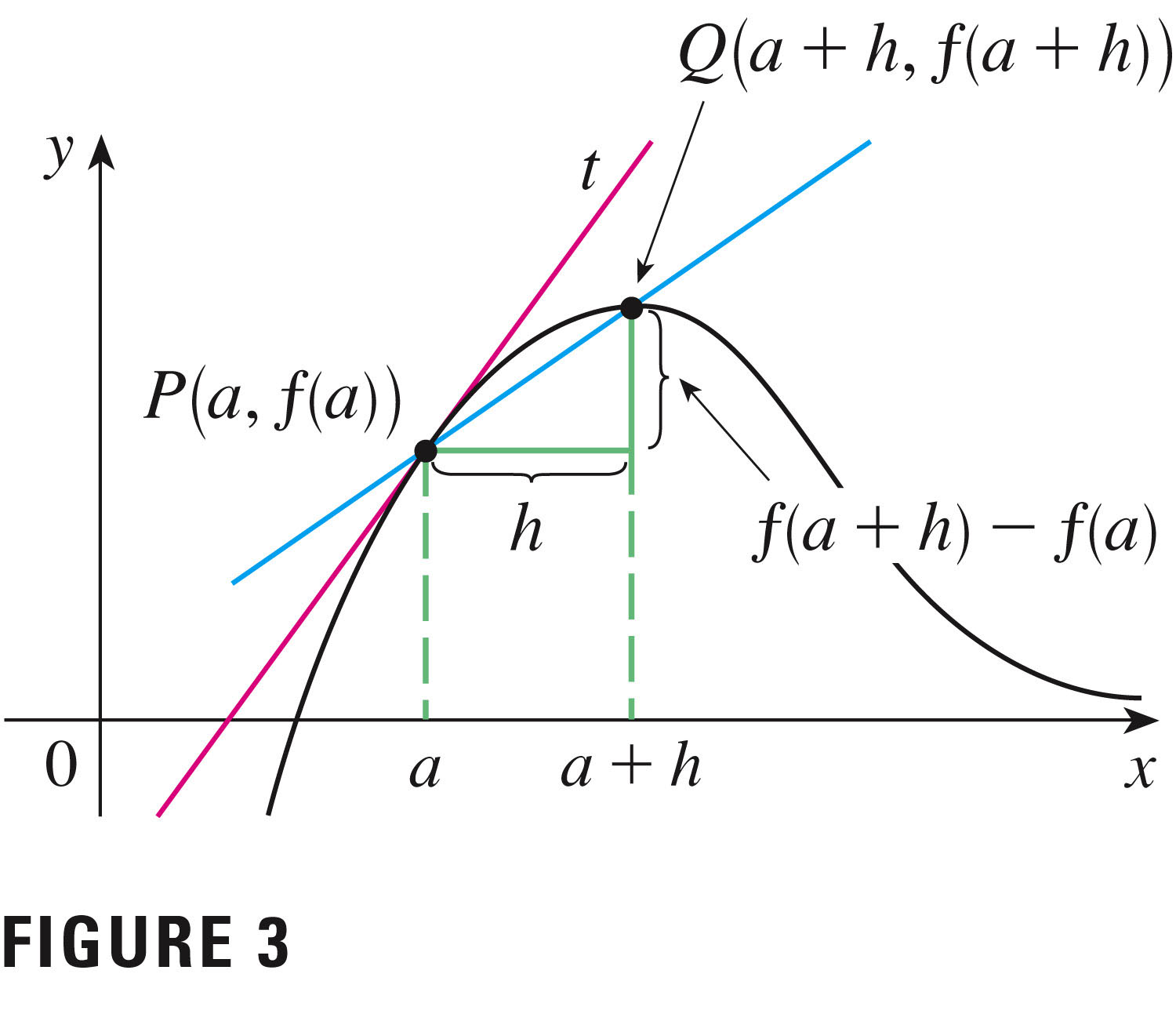

Here's an alternative notation for the slope: The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment, $\frac{f(a+h)-f(a)}{h}$ In the limit, this is $m=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$ which I call the most important definition in calculus. This is the formula for the derivative at a point: I've already shared with you the definition of the derivative function, at any value of $x$.

$f^\prime(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} = \lim_{x \to a} \frac{f(x)-f(a)}{x-a}$

The most important definition in calculus! (I just can't say it enough!)

Now let's look at some problems, and see how this concept is connected to real-world problems.

• #3, pp. 110
• #11, pp. 111
• #13, pp. 111
• #29, pp. 112
• #51, pp. 113