- You have a homework due Monday.
- We'll have a quiz at the end of the hour.
- Theorem: Suppose that f is continuous on the closed
interval [a,b] and let N be any number between
f(a) and f(b), where $f(a)\ne{f(b)}$. Then there exists a
number $c$ in $(a,b)$ such that $f(c)=N$.
- Example: pp. 93, #69
Define $D(t)$ to be the difference in position between the two days. At the outset, at $t=7am$, it's equal to the height of climb (call it $H$). By the end of the day, at $t=7pm$, it's equal to the negative of the height.
Since the difference in heights is connected (continuous), there must be a point in time $T$ at which $D(T)=0$, which is one point at which the Tibetan monk is at the same place on the trail at the same time (by the IVT).
- We lead into the derivatives by discussing secants, tangents, limits.
- Secants can be used with limits to lead to tangent lines (places where a line osculates -- kisses -- a curve).
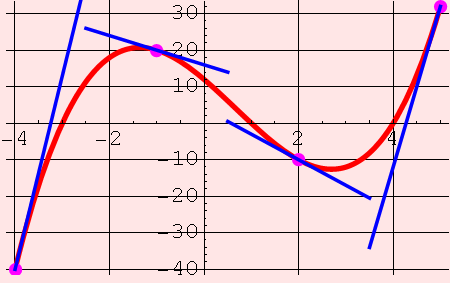
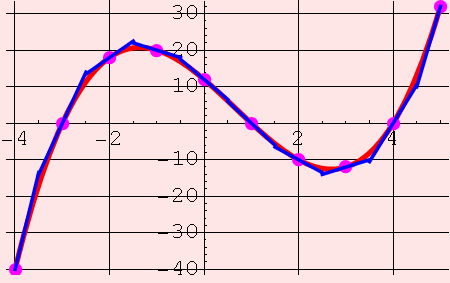
These are "rates of change" of the function f. What does that mean? The thing that tells you how fast a function is changing is its slope, isn't it? If a function is constant, then it's not changing at all. If the slope is steep (either up or down), then the function's values are changing dramatically and quickly.
The rate of change is dictated by the slope. So it should come as no surprise that the derivative of a function at a point is the same as the slope of the tangent line at a point:
There can be some important exceptions to or problems with this rule of slopes of tangent lines:
So let's obtain the slope of the tangent line using limits of secant lines, in two different ways:
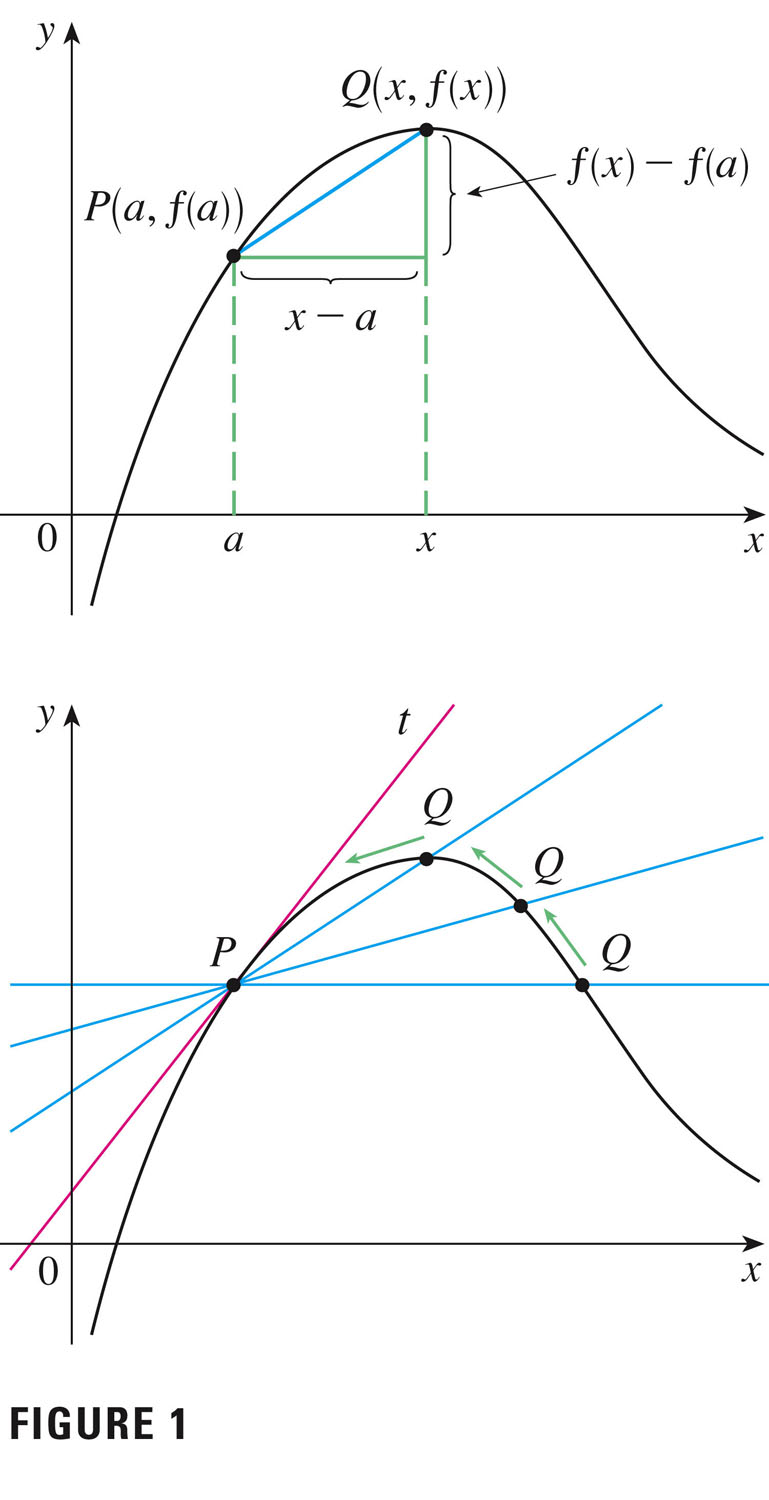
The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment (the slope of a secant line), $\frac{f(x)-f(a)}{x-a}$ This is an average rate of change in f over a finite interval.
In the limit, this average rate of change becomes an instantaneous rate of change:
$m=\lim_{x\to{a}}\frac{f(x)-f(a)}{x-a}$ 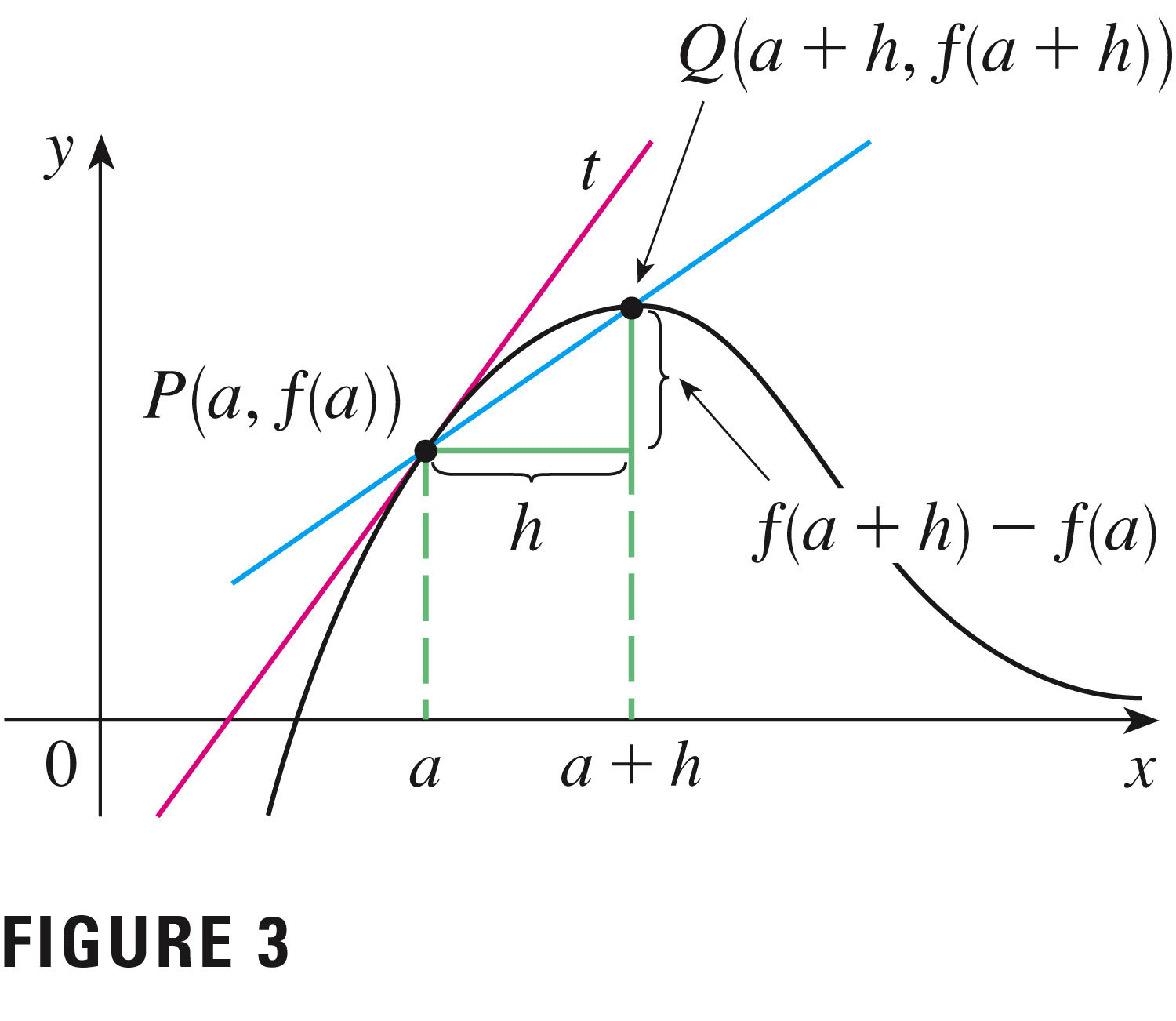
Here's an alternative notation for the slope: The slope m of the tangent line at P(a,f(a)) is approximated by the slope of the blue line segment,
$\frac{f(a+h)-f(a)}{h}$ In the limit, this is
$m=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$ which I call the most important definition in calculus. This is the formula for the derivative at a point: I've already shared with you the definition of the derivative function, at any value of $x$.
- Definition of the derivative at a point: well, it's just a slope, isn't it:
$f^\prime(a) = \lim_{h \to 0} \frac{f(a+h)-f(a)}{h} = \lim_{x \to a} \frac{f(x)-f(a)}{x-a}$
The most important definition in calculus! (I just can't say it enough!)
Now let's look at some problems, and see how this concept is connected to real-world problems.
- #3, pp. 110
- #11, pp. 111
- #13, pp. 111
- #29, pp. 112
- #51, pp. 113