Day 16, Mat128: Calculus A

• Make sure that you label your graphs.
• As usual, follow directions: you were to provide a function....

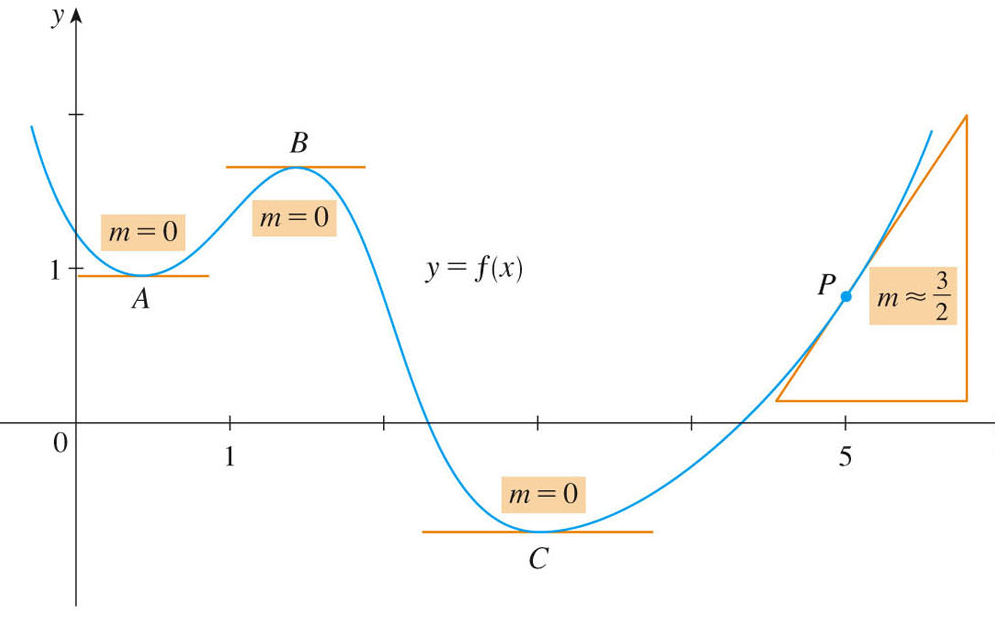
Let's think about how to graph the derivative function of this function.

So, from the slopes, one constructs a function: the derivative function. The derivative function gives the slope of the tangent line at a point in the domain where the function is smooth, and where, should you zoom in, you'll eventually see what looks like a straight line (the tangent line).

We see the derivative (thought of as a slope) at four separate points (A, B, C, and P). At three of these points we see that the slope (and hence the derivative) is zero. These are especially important points, since, as you can see, the function achieves its extreme values on a local level at these points. That's something we are often interested in -- when is a function at its peak or pit?

One of the local peaks or pits may be global as well, and if we were looking for the place along the $x$-axis where the minimum of the function occurs, we might guess $x=3$. There may be no maximum, as the values of the function on the boundary are largest (that we can see).

We can see, however, that the slope is perfectly well defined everywhere for this function (with the possible exception of the end points, where the graph disappears, and we won't have limits from left and right). Now let's see how to draw a rough approximation to the derivative function in this case.

How well can you recognize derivatives and the functions that give rise to them?

Last time we used the definition of the derivative function,

\[ f^\prime(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]

to determine the derivative functions of these important functions:

1. Constant functions: $f(x)=c$
2. Linear functions: $f(x)=mx+b$
3. Quadratic functions: $f(x)=ax^2+bx+c$

4. An important application of the tangent line

We also had a look at #3, p. 122. Let's review, thinking in particular about the symmetry, and a conjecture: that the derivative function of a polynomial is also a polynomial, of degree one lower.

If a function's derivative is another function, does that function have a derivative?

The derivative of the derivative of a function is called the second derivative of that function. And how do we interpret these "higher derivatives" in the context of a motion?

Let's think of a quadratic motion, e.g. the motion of an eraser thrown across the room. Let s be the height of the eraser:

$s(t)=at^2+bt+c$

Each of the coefficients has an important, intuitive role to play:

• $c$ is the height at time $t=0$;
• $b$ is the rate of change in height at time $t=0$;
• $2a$ is the acceleration (due to gravity) of the height.

So

$s'(t)=2at+b$, and

$s''(t)=2a$.

$s'''(t)=0$.

We can continue, of course, and so we see that

$s^{(n)}(t)=0$ for all $n>2$.

\[ f^\prime(x) = \frac{dy}{dx} = \frac{d}{dx}\left(f(x)\right)=\left(f(x)\right)'=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]

There are several different ways of writing the derivative, and you need to get used to them. The third and fourth forms remind us that differentiation is itself a function: it takes a function in its domain and returns another function in its range -- the derivative function.

• #2, p. 122 (so, So, from slopes, one constructs a derivative function)
• #25 (using "the most important definition in calculus"; note the slightly different domains)
• #48, p. 125.

• Rules that help us avoid having to use the definition each time (with Proofs):
  • The constant multiple rule (makes sense)
    $(cf(x))'=cf'(x)$

  • The sum rule

    works as we'd hope: "The derivative of a sum is the sum of the derivatives."

    $(f(x) + g(x))'=f'(x)+g'(x)$

  • The power rule (via dominoes -- i.e., mathematical induction -- or via the binomial theorem)
    $(x^n)'=n x^{n-1}$

  • NOTE: at this point we have all the rules necessary to differentiate all polynomials, without needing to resort to the definition!

    The derivative of the monomial $x^n$ is $nx^{n-1}$, and

    The derivative of the monomial $c x^n$ is $nc x^{n-1}$ (by constant multiple).

    A polynomial is just a sum of these. So we apply the sum rule, and the power rule, and the constant multiple rule to the flight of the eraser, to get

    $s'(t)=(at^2+bt+c)'=2at+b$

    and

    $s''(t)=(2at+b)'=2a$

• Other rules:
  • The product rule (doesn't work the way we'd hope):
    $(f(x) \cdot g(x))'=f'(x)g(x)+f(x)g'(x)$

  • The quotient rule:
    low d high minus high d low,
    over the denominator squared they go.

    $\left(\frac{f(x)}{g(x)}\right)'=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}$

• #13, p. 136
• #22, p. 136 (expand first)
• #48, p. 137
• #58, p. 137