- Your exams are returned.
- Your Platonic solid homework is due, but I'll collect it next time. We're not in a hurry, and I want to say a little more about Platonics today.
- Here they are, in all their glory:
The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia! Tetrahedron Hexahedron
or CubeOctahedron Dodecahedron Icosahedron 




A few more "applications" (or examples) of Platonic solids in our world:
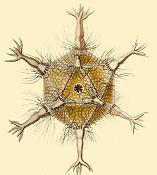
- Icosahedron
- amoeboid protozoa (Circogonia icosahedra)
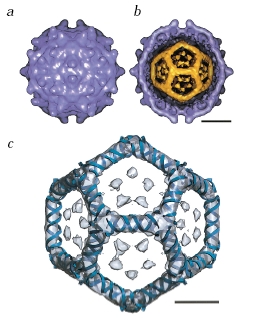
- Viruses:
- The Cliff Notes Version...

"An array of viruses. (a) The helical virus of rabies. (b) The segmented helical virus of influenza. (c) A bacteriophage with an icosahedral head and helical tail. (d) An enveloped icosahedral herpes simplex virus. (e) The unenveloped polio virus. (f) The icosahedral human immunodeficiency virus with spikes on its envelope."
- Bacteriophages and Virions
- The Cliff Notes Version...
- Dodecahedral
- amoeboid protozoa (Circogonia icosahedra)
- More critters:
- Icosahedron
- Now let's fill in the following table about the Platonic solids:
# of Vertices Edges Faces faces at each vertex sides at each face Tetrahedron Cube Octahedron Dodecahedron Icosahedron What conclusions can we draw from this data? Is there a pattern? (Of course there is!:) The table possesses a certain symmetry. The pattern leads to the concept of "Duality":
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.


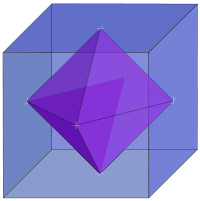
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.