Day 33, Mat129: Calculus I

Last time:

Next time:

Today:

Announcements
- Your 3.9 homework is returned: graded 4, 35, 53
  - #4: $\frac{8}{10}=\frac{4}{5}$. Simplify when it's easy!
  - #35, 53: some of you switched from $\theta$ or $t$ to $x$ (our favorite independent variable). Love the one you're with!
- We have our third midterm exam coming up, next Monday.
  I'm going to drop the lowest of your three midterms. That's not an excuse to blow this one off, but rather an opportunity to improve on your test average.
  The test will cover up from 3.3 through 4.2, which we basically finished last time.
section 4.2: The definite integral
- This section generalizes our intuition and examples from the preceding section:
  - First of all, we can't expect our function to be positive all the time, so we define "signed area":
    
    and then we give a name to this area:
  - The area can be calculated by chopping the interval [a,b] up into smaller and smaller chunks, and then using rectangular approximations to the small areas.
    If the size of the intervals goes to zero, then the approximations get better and better, until they're perfect!
    Assuming that we use equal-sized subintervals, the definite integral of $f$ from $a$ to $b$ is defined by \[ \int_{a}^{b}f(x)dx = \lim_{n \to \infty}\sum_{i=1}^{n}f(x_i^*)\Delta x \] where the $x_i^*$ are sample points, one from each of the $n$ rectangles of width $\Delta x = \frac{b-a}{n}$.
    
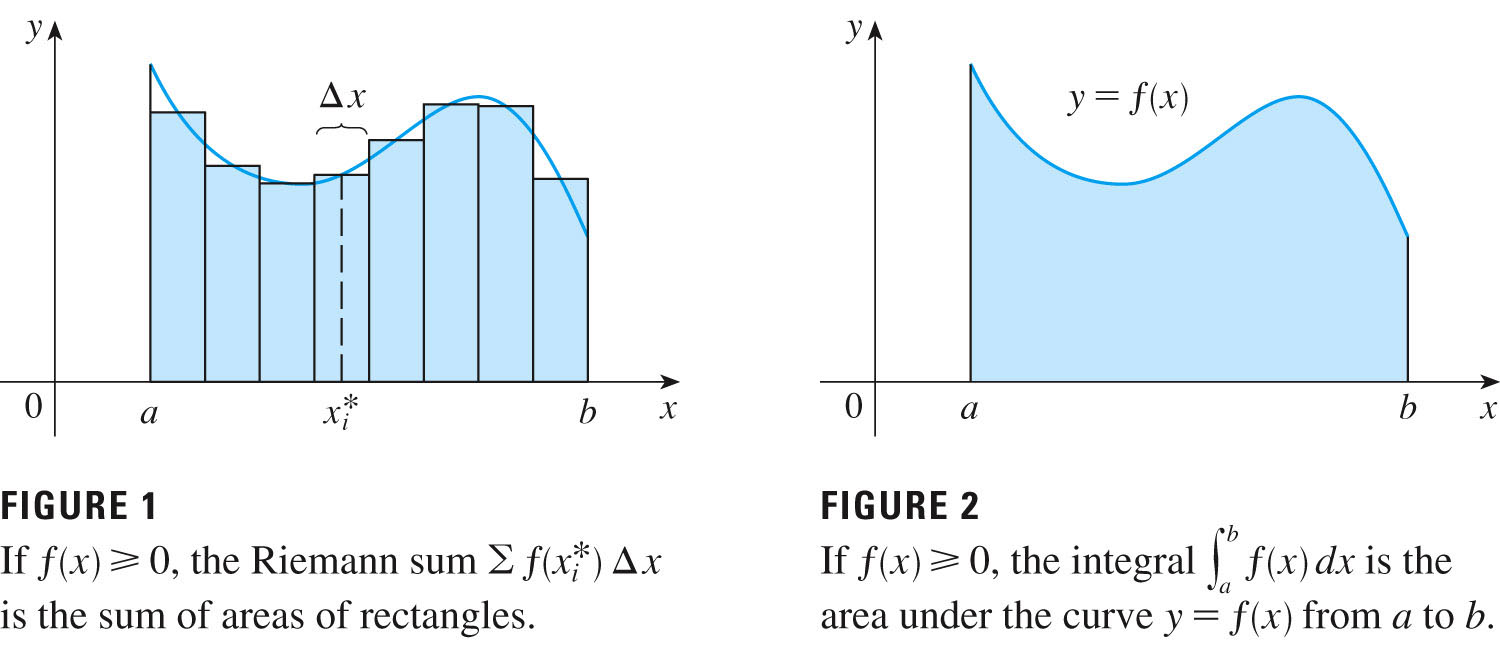
    Theorem 3, p. 297, tells us that this integral will be defined ($f$ is integrable) whenever $f$ is continuous (or has at most a finite set of discontinuities).
    Theorem 4, p. 298, tells us that we can take RRR as our method and be assured of getting the right answer. But we could just as well use the LRR, or midpoint, or trapezoidal, etc.
  - Properties of the Definite Integral:
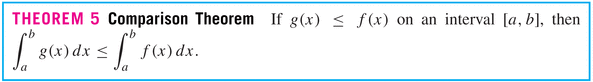
  - Here's how we'd rewrite our generalization that Area under the graph of f from a to b =
    width of the interval times the average value =
    $(b-a)\bar{f}$
    where by
    $\bar{f}\mbox{}$
    we mean an average value of f. So
    $\int_{a}^{b}f(x)dx=\bar{f}(b-a)$
  - Examples:
    - #7, p. 306
    - #10
    - #21 (see p. 298 for the equations you might need, and example 2)
    - #33
Section 4.3: the Fundamental theorem of calculus
- Well folks, here it is: the fundamental theorem, that ties together integral and differential calculus. It comes in two parts:
  1. If $f$ is continuous on $[a,b]$, then
    $\int_{a}^{b}f(x)dx=F(b)-F(a)$
    where $F$ is any antiderivative of $f$; that is, a function such that $F'=f$.
  2. If $f$ is continuous on $[a,b]$, then the function $F$ defined by \[ F(x)=\int_{a}^{x}f(t)dt \;\;\;\;\; a \le x \le b \] is continuous on $[a,b]$ and differentiable on $(a,b)$, and $F'(x)=f(x)$.
  It says that to integrate, all you have to do is think of an antiderivative F of the integrand f.
- Let's derive/motivate the FTC using the linearization.
- Examples:
  - #3, p. 318
  - #22
  - #23
  - #8
  - #13 (a composition, requiring the chain rule)
  - #58
Now on to Section 4.4: the indefinite integral:
- Not too much to shout about here: the indefinite integral represents the family of anti-derivatives of a function:
  
  $\int{f(x)dx}=F(x)+C$
  where $F(x)$ is any particular anti-derivative.
Let me bring to your attention the table of integrals at the back of the book. This is basically a table of functions and their antiderivatives.
Examples:
- #1, p. 326
- #5
- #45
- #50; furthermore, what does
  
  $100+\int_{0}^Tn'(t)dt$
  represent?

Website maintained by Andy Long. Comments appreciated.