- Your 1.8 homework is returned. I graded them all -- let's talk about the intermediate value theorem!
- For some of you, the Intermediate Value Theorem (IVT) is
so obvious that you don't get it: what is there to say? Well,
whenever you want to use a theorem, you need to satisfy the
conditions of the theorem. So you'll need a continuous function
$f$, whose value will be $N$ at some value $x=c$ in the
domain; and you'll need to show that $f$ takes values both
below and above $N$, so that $N$ is intermediate between
them!
Let's look at #54: it's kind of like the Tibetan monk problem, in that we had to create a single function from the two functions (up and down).
- For some of you, the Intermediate Value Theorem (IVT) is
so obvious that you don't get it: what is there to say? Well,
whenever you want to use a theorem, you need to satisfy the
conditions of the theorem. So you'll need a continuous function
$f$, whose value will be $N$ at some value $x=c$ in the
domain; and you'll need to show that $f$ takes values both
below and above $N$, so that $N$ is intermediate between
them!
- You've got 2.1 homework due Thursday; 2.2 is due 2/5.
- We'll also have a quiz Thursday, over sections 2.1 and 2.2.
- Your first exam is next week, Thursday, 2/8, and will cover up
through section 2.2.
- Please put your rectangles away.
-
Definition: A function $f$ is differentiable at $a$ if the derivative $f^\prime(a)$
exists. It is differentiable on an open interval $(a,b)$ [or
$(a,\infty)$ or $(-\infty,a)$ or $(-\infty,\infty)$] if it is differentiable at
every number in the interval.
- If $f$ is differentiable at $a$, then $f$ is continuous at $a$.
- But the converse is not true: just because $f$ is continuous at
$a$ does not mean that it is differentiable there.
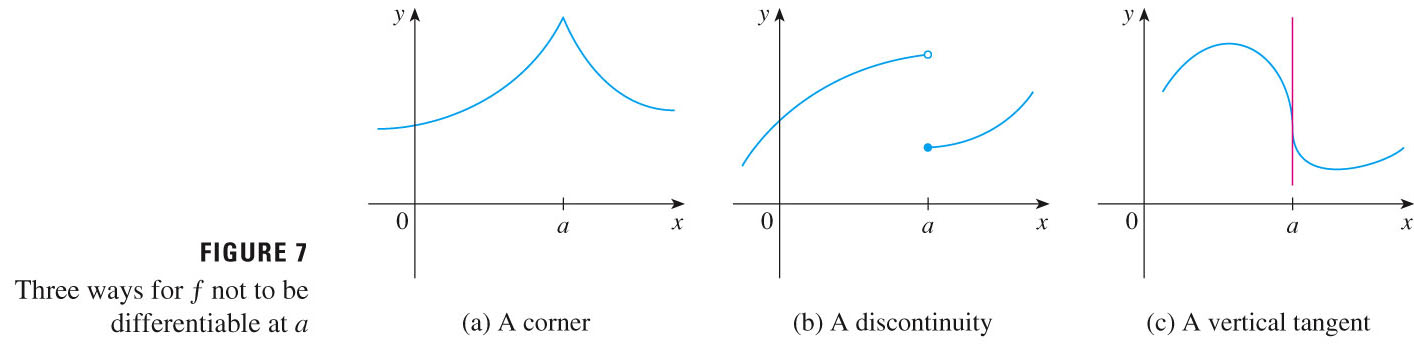
- Differentiability on an interval implies continuity and smoothness.
Let's use the definition of the derivative function,
\[ f^\prime(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]
to determine the derivative functions of these important functions:
- Constant functions: $f(x)=c$
- Linear functions: $f(x)=mx+b$
- Quadratic functions: $f(x)=ax^2+bx+c$
- An important application of the tangent line
The first two derivatives are easy: each function has a straight line graph, so the tangent line is the graph of the function itself. The slope of each of those graphs is easy to see (either 0 or m). The derivatives are hence on full display. Not so much for the quadratic, and it's the first function that has an explicit dependence on $x$.
How well can you recognize derivatives and the functions that give rise to them? Let's try #3, p. 122.
Some thoughts:- What causes breaks in derivative functions?
- How is symmetry preserved in derivatives?
- How does the degree of a polynomial change under differentiation?
-
The derivative of the derivative of a function is called the second
derivative of the function, and denoted $f''(x)$. And how do we interpret these "higher
derivatives" in the context of a motion?
Let's think of a quadratic motion, e.g. the motion of an eraser thrown across the room. Let $s(t)$ be the height of the eraser at time $t$:
\[s(t)=at^2+bt+c\]
Each of the coefficients has an important, intuitive role to play:
- $c$ is the initial height, at time $t=0$;
- $b$ is the initial velocity, the rate of change of height at time $t=0$;
- $2a$ is the acceleration (due to gravity) of the height (the
derivative of the velocity is acceleration).
- It is constant across this motion, if we neglect other forces (e.g. air resistance), or the fact that gravity is actually a function of the distance from the center of the Earth.
- Forces result in accelerations (and vice versa, per Newton's equation $f=ma$).
Example: So in problem #13, p. 111, a ball was thrown into the air with a velocity of 40 ft/s, and its height (in feet) is given by h \[s(t)=40t-16t^2\] So its initial height is 0; its initial velocity is 40 ft/s (up, against the force of gravity); and the acceleration is 2*(-16)=-32 ft/s/s (note the units). The acceleration is in the direction opposite the velocity, pointing downward. That's why it's negative.Think about the parabola which is this function's graph: it's an umbrella. The ball will rise, reach its apex, then fall back to Earth.
\[s(t)=40t-16t^2\] \[s'(t)=v(t)=40-32t\]
\[s''(t)=v'(t)=a(t)=-32\]
Blue -- graph of $s(t)$ Red -- graph of $s'(t)$
Of course we could continue on and define higher derivatives (third, fourth, etc.). The notation for the $n^{th}$ derivative is frequently $f^{(n)}(x)$.The parentheses are supposed to tip you off to the fact that these aren't powers, but rather derivatives.
- Here are other notations for the derivative function:
\[ f^\prime(x) = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx}\left(f(x)\right)=\left(f(x)\right)'=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]
There are several different ways of writing the derivative, and you need to get used to them. The form \(\frac{d}{dx}\left(f(x)\right)\) reminds us that the operation of differentiation is itself a function: it takes a function in its domain and returns another function -- the derivative function.
- Examples:
- #2, p. 122 (so, from slopes, one constructs a derivative function)
- #25 (using "the most important definition in calculus"; note the slightly different domains)
- #48, p. 125.
- So the algebra was really ugly to use the definition to
find the derivative of that radical function in #25. That was
nasty, wasn't it? Wouldn't it be nice if we could avoid all of that?
Well we can, using some rules that are derived from the limit
definition of the derivative.
- So now we'll use the definition of the derivative to prove
several of the formulas in this section. We've already proven
the first two rules (constant functions $f(x)=c$ and the
linear function $f(x)=x$).
- Rules that help us avoid having to use the definition each time
(with Proofs):
- The constant multiple rule (makes sense)
$(cf(x))'=cf'(x)$ -
- The sum rule
- works as we'd hope: "The derivative of a sum is the sum of the derivatives."
$(f(x) + g(x))'=f'(x)+g'(x)$ - The product rule (doesn't work the way we'd hope):
$(f(x) \cdot g(x))'=f'(x)g(x)+f(x)g'(x)$ To prove it we use one of my favorite tricks: the addition of a special form of 0.
- The power rule:
$(x^n)'=n x^{n-1}$ where $n$ is a positive integer.
We can prove this via dominoes -- i.e., mathematical induction -- or via the binomial theorem)
- NOTE: at this point we have all the rules necessary
to differentiate all polynomials, without needing to
resort to the definition!
The derivative of the monomial $x^n$ is $nx^{n-1}$, and
The derivative of the monomial $c x^n$ is $nc x^{n-1}$ (by constant multiple).
A polynomial is just a sum of these. So we apply the sum rule, and the power rule, and the constant multiple rule to the flight of the eraser, to get
$s'(t)=(at^2+bt+c)'=2at+b$
and
$s''(t)=(2at+b)'=2a$
- The constant multiple rule (makes sense)
- Other rules:
- The quotient rule:
low d high minus high d low,
over the denominator squared they go.$\left(\frac{f(x)}{g(x)}\right)'=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}$
- The quotient rule:
- Rules that help us avoid having to use the definition each time
(with Proofs):
- Examples:
- #13, p. 136
- #22, p. 136 (expand first)
- #48, p. 137
- #58, p. 137