- Your quiz is returned.
- Your 1.8 homework is due.
- You've got 2.1 homework due Thursday; 2.2 is due 2/5.
- Your first exam is next week, and will cover through section 2.2.
- Please put your rectangles away.
-
Definition: A function $f$ is differentiable at $a$ if the derivative $f^\prime(a)$
exists. It is differentiable on an open interval $(a,b)$ [or
$(a,\infty)$ or $(-\infty,a)$ or $(-\infty,\infty)$] if it is differentiable at
every number in the interval.
- If $f$ is differentiable at $a$, then $f$ is continuous at $a$.
- But the converse is not true: just because $f$ is continuous at
$a$ does not mean that it is differentiable there.
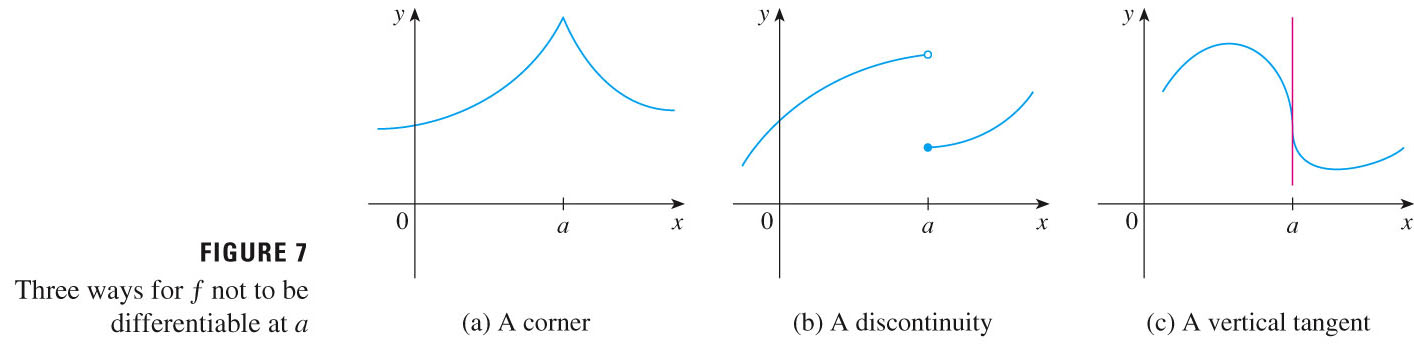
- Differentiability on an interval implies continuity and smoothness.
Let's use the definition of the derivative function,
\[ f^\prime(x) = \lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]
to determine the derivative functions of these important functions:
- Constant functions: $f(x)=c$
- Linear functions: $f(x)=mx+b$
- Quadratic functions: $f(x)=ax^2+bx+c$
- An important application of the tangent line
The first two derivatives are easy: each function has a straight line graph, so the tangent line is the graph of the function itself. The slope of each of those graphs is easy to see (either 0 or m). The derivatives are hence on full display. Not so much for the quadratic, and it's the first function that has an explicit dependence on $x$.
How well can you recognize derivatives and the functions that give rise to them? Let's try #3, p. 122.
Some thoughts:- What causes breaks in derivative functions?
- How is symmetry preserved in derivatives?
- How does the degree of a polynomial change under differentiation?
-
The derivative of the derivative of a function is called the second
derivative of the function, and denoted $f''(x)$. And how do we interpret these "higher
derivatives" in the context of a motion?
Let's think of a quadratic motion, e.g. the motion of an eraser thrown across the room. Let $s(t)$ be the height of the eraser at time $t$:
\[s(t)=at^2+bt+c\]
Each of the coefficients has an important, intuitive role to play:
- $c$ is the initial height, at time $t=0$;
- $b$ is the initial velocity, the rate of change of height at time $t=0$;
- $2a$ is the acceleration (due to gravity) of the height (the
derivative of the velocity is acceleration).
- It is constant across this motion, if we neglect other forces (e.g. air resistance), or the fact that gravity is actually a function of the distance from the center of the Earth.
- Forces result in accelerations (and vice versa, per Newton's equation $f=ma$).
Example: So in problem #13, p. 111, a ball was thrown into the air with a velocity of 40 ft/s, and its height (in feet) is given by h \[s(t)=40t-16t^2\] So its initial height is 0; its initial velocity is 40 ft/s (up, against the force of gravity); and the acceleration is 2*(-16)=-32 ft/s/s (note the units). The acceleration is in the direction opposite the velocity, pointing downward. That's why it's negative.Think about the parabola which is this function's graph: it's an umbrella. The ball will rise, reach its apex, then fall back to Earth.
\[s(t)=40t-16t^2\] \[s'(t)=v(t)=40-32t\]
\[s''(t)=v'(t)=a(t)=-32\]
Blue -- graph of $s(t)$ Red -- graph of $s'(t)$
Of course we could continue on and define higher derivatives (third, fourth, etc.). The notation for the $n^{th}$ derivative is frequently $f^{(n)}(x)$.The parentheses are supposed to tip you off to the fact that these aren't powers, but rather derivatives.
- Here are other notations for the derivative function:
\[ f^\prime(x) = \frac{dy}{dx} = \frac{df}{dx} = \frac{d}{dx}\left(f(x)\right)=\left(f(x)\right)'=\lim_{h \to 0} \frac{f(x+h)-f(x)}{h} \]
There are several different ways of writing the derivative, and you need to get used to them. The form \(\frac{d}{dx}\left(f(x)\right)\) reminds us that the operation of differentiation is itself a function: it takes a function in its domain and returns another function -- the derivative function.
- Examples:
- #2, p. 122.
- #23, p. 124
- #25
- #48, p. 125.