- There's a quiz today at the end of the hour, over the trig stuff.
- Please put your rectangles away.
- The chain rule is so critically important because of the
importance of compositions of functions: for
$F(x) = f(g(x))$,
$F^\prime(x) = f^\prime(g(x))g^\prime(x)$ I personally think this to myself: "f prime of stuff times the derivative of the stuff"; or "f prime of stuff times stuff prime.",
where $f$ is the "outside" function:
$F^\prime(x) = f^\prime(stuff)stuff^\prime$ You can see that the rule is fairly simple, once you've identified the composition -- that is, once you've torn apart $F$ to find $f$ and $g$.
You might take a look at this summary from my pre-calc class to review compositions.
- In Leibniz notation, if $y=f(u)$ and $u=g(x)$ are both differentiable
functions, then
\[
\frac{dy}{dx} = \frac{dy}{du} \frac{du}{dx}
\]
This alternative version of the formula helps us to remember that $x$
is going on a journey, passing first through $g$ to become something
new ($u=g(x)$), and then continues on as $u$ through the function $f$
to become $y=f(u)$. It's a metamorphosis. It should be called
the "metamorphosis rule", if there were any justice in the world....
- The difficulty is often identifying the composition. We'll try
some easy ones first, then get to some ugly ones.
Before we do that, however, I'd like to motivate (rather than prove) the chain rule, using the limit definition of the derivative. Everything comes from that!
Basically, however, it relies on the tangent line: we want to use the fact that
$f(x+h) \approx f(x) + hf'(x)$ Why does that make sense? Because it comes straight out of the limit definition, where we throw away the limit. That's why we have to write "$\approx"$:
$f'(x) \approx \frac{f(x+h)-f(x)}{h}$ - #9, p. 154
- #16
- #29 -- the chains can get longer!
- #77
- A Chain Rule tutorial
- A sample problem involving compositions: model the seasonal variation in Keeling's CO2 data:
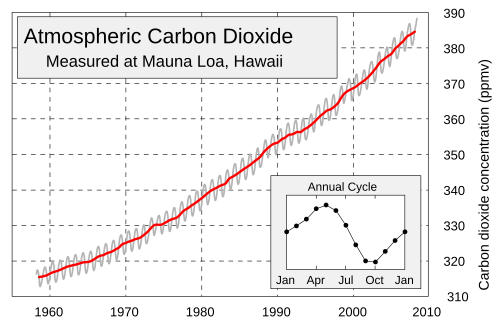
- Keeling data with models:
If time were measured in years from January, would
$V(t)=A\sin(2\pi{t})$ be a good model? What would be a good choice for the parameter $A$?
We'll approach this topic via some examples:
- Consider the relationship between x and y given by
$y = \frac{1}{x}$ We know how to differentiate y with respect to x, using the power rule.
But there's another way to think about this relationship, and that's
$x y =1$ This gives no priority to either variable. We can still differentiate to find y'(x), however, using the product rule and something called "implicit differentiation". We consider $y$ and unknown (implicitly defined) function of $x$, treating it as $y(x)$; then, since both sides of the equation
$x y(x) =1$ are equal, the derivatives of both sides must be equal. We differentiate both sides, and equate them (using the product rule on the left). From this we obtain the correct derivative, as well.
The solution curves are hyperbolas (one of the conic sections).
- Another example is the folium of Descartes, which is the graph
(solution) of the implicit equation
but\[
x^3 + y^3 = 6xy
\]
Here the equation is perfectly symmetric in $x$ and $y$: it's not at all clear
which variable is dependent, and which independent. By the way, this
symmetry in $x$ and $y$ means that the
solution curve must be symmetric about the line $\displaystyle y=x$. See
Figure 4, p. 159:
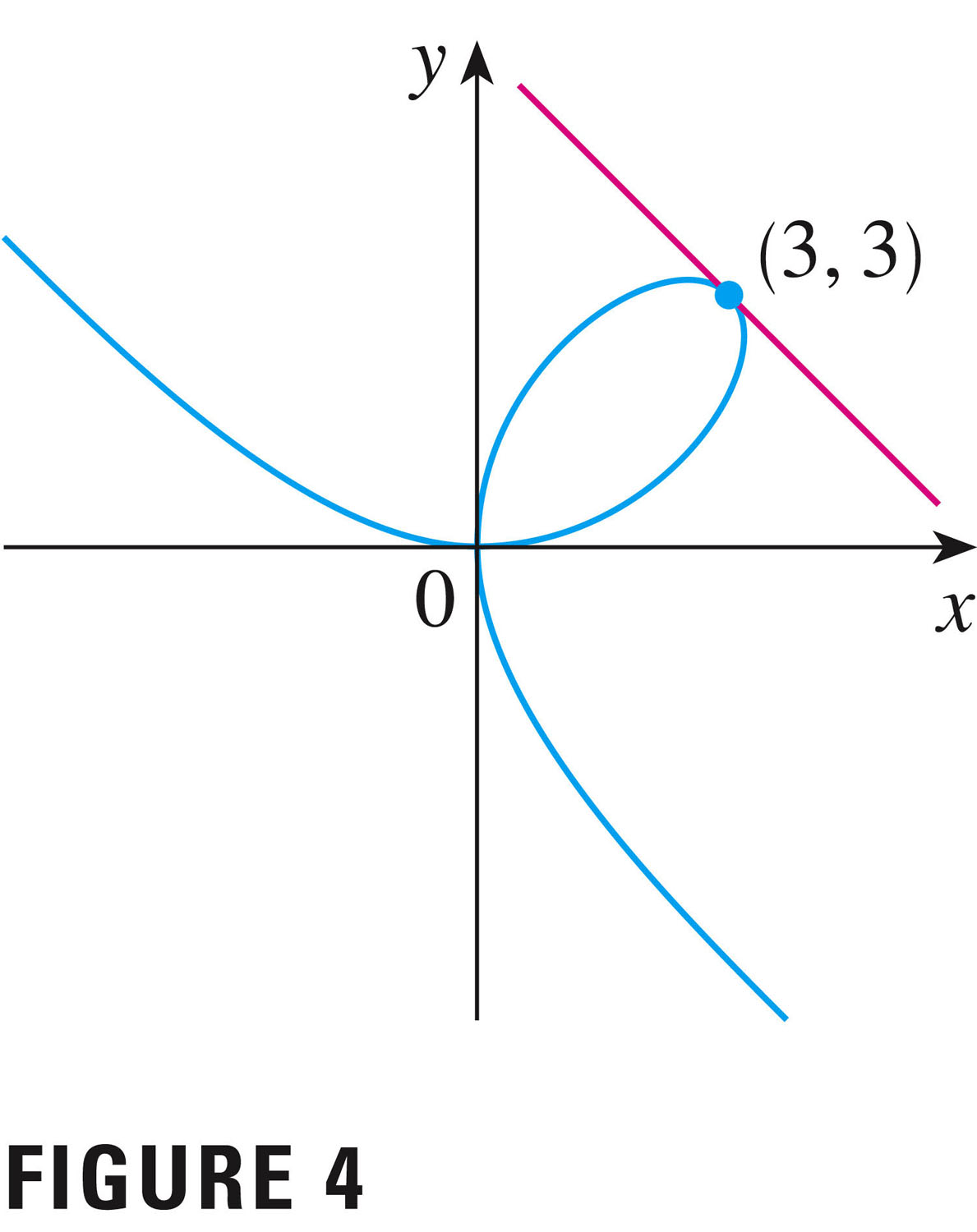
Even though the graph is not the graph of a function (either $y(x)$ or $x(y)$), we can still find tangent lines, etc., using ordinary derivatives. It is the case, however, that a single point in the plane can be represented by several different tangent lines (e.g. the point (0,0)).
- Here's a more complicated relationship between x and y given by
$x^2+y^2=(2x^2+2y^2-x)^2$ (#29, p. 162):
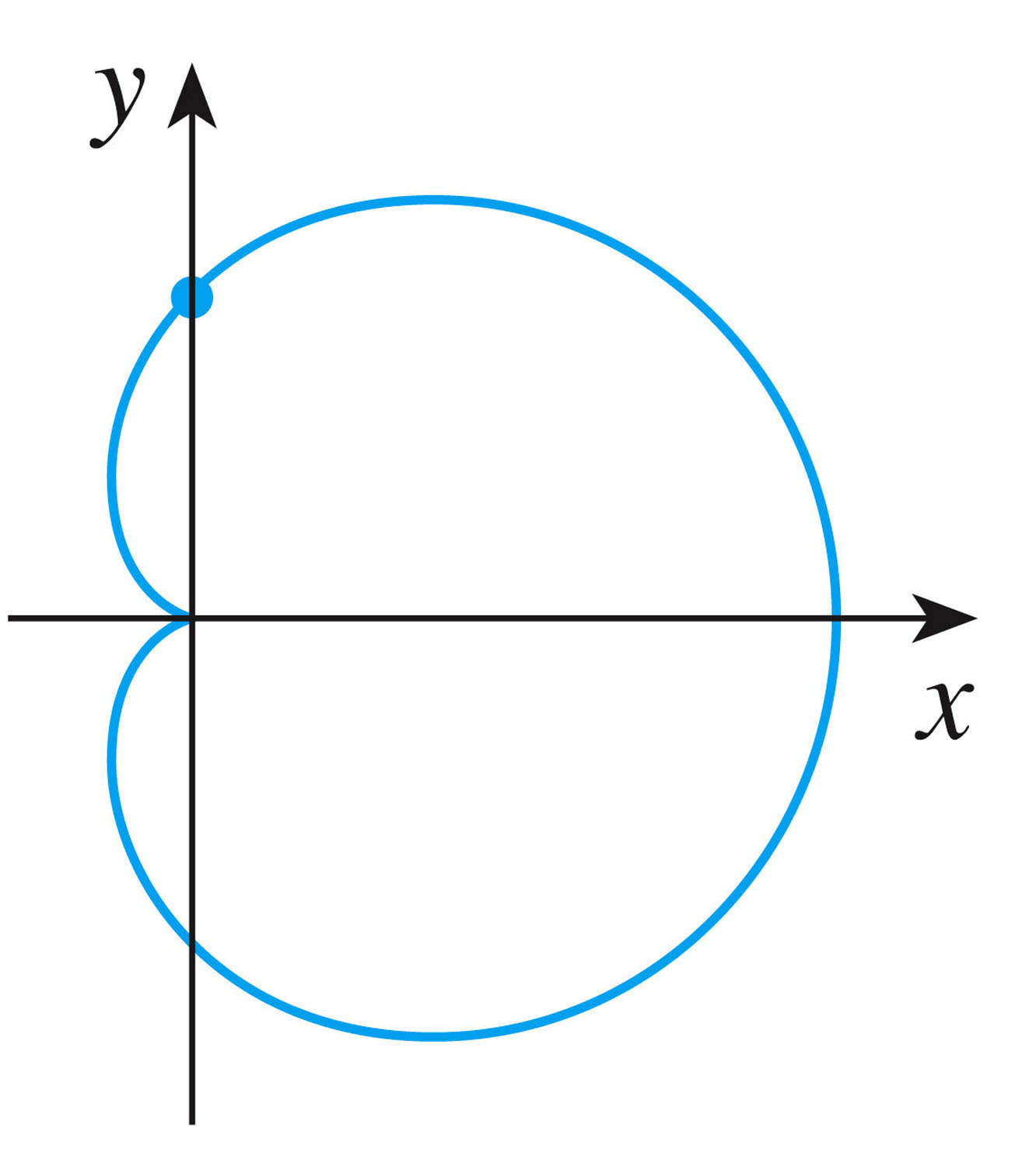
Because the equation is symmetric in $y$ (even in $y$), we expect the curve to be a reflection about the $x$-axis (as it is).
- Let's look at one important application of implicit functions: orthogonal families. #49, p. 163.