- Your quiz is returned.
- Your 2.4 homework is due today.
- Please put your rectangles away.
Implicit differentiation makes use of the chain rule, so it's a good topic to have follow right on its heels.
We approached the topic via some examples:
- Consider the relationship between x and y given by
$y = \frac{1}{x}$ We know how to differentiate y with respect to x, using the power rule.
But there's another way to think about this relationship, and that's
$x y =1$ This gives no priority to either variable. We can still differentiate to find y'(x), however, using the product rule and something called "implicit differentiation". We consider $y$ and unknown (implicitly defined) function of $x$, treating it as $y(x)$; then, since both sides of the equation
$x y(x) =1$ are equal, the derivatives of both sides must be equal. We differentiate both sides, and equate them (using the product rule on the left). From this we obtain the correct derivative, as well.
The solution curves are hyperbolas (one of the conic sections).
- Another example is the folium of Descartes, which is the graph
(solution) of the implicit equation
but\[
x^3 + y^3 = 6xy
\]
Here the equation is perfectly symmetric in $x$ and $y$: it's not at all clear
which variable is dependent, and which independent. By the way, this
symmetry in $x$ and $y$ means that the
solution curve must be symmetric about the line $\displaystyle y=x$. See
Figure 4, p. 159:
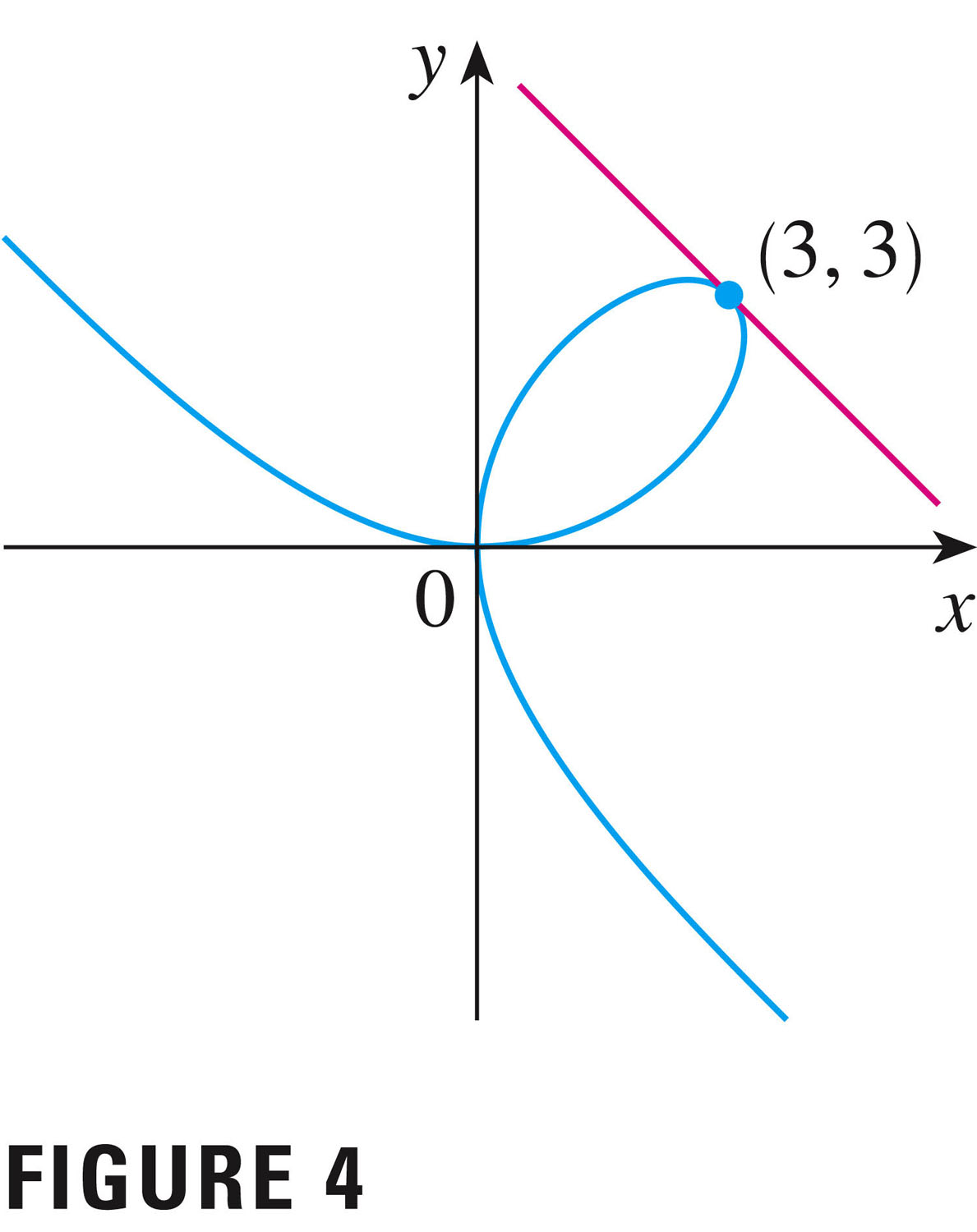
Even though the graph is not the graph of a function (either $y(x)$ or $x(y)$), we can still find tangent lines, etc., using ordinary derivatives. It is the case, however, that a single point in the plane can be represented by several different tangent lines (e.g. the point (0,0)).
- Here's a more complicated relationship between x and y given by
$x^2+y^2=(2x^2+2y^2-x)^2$ (#29, p. 162):
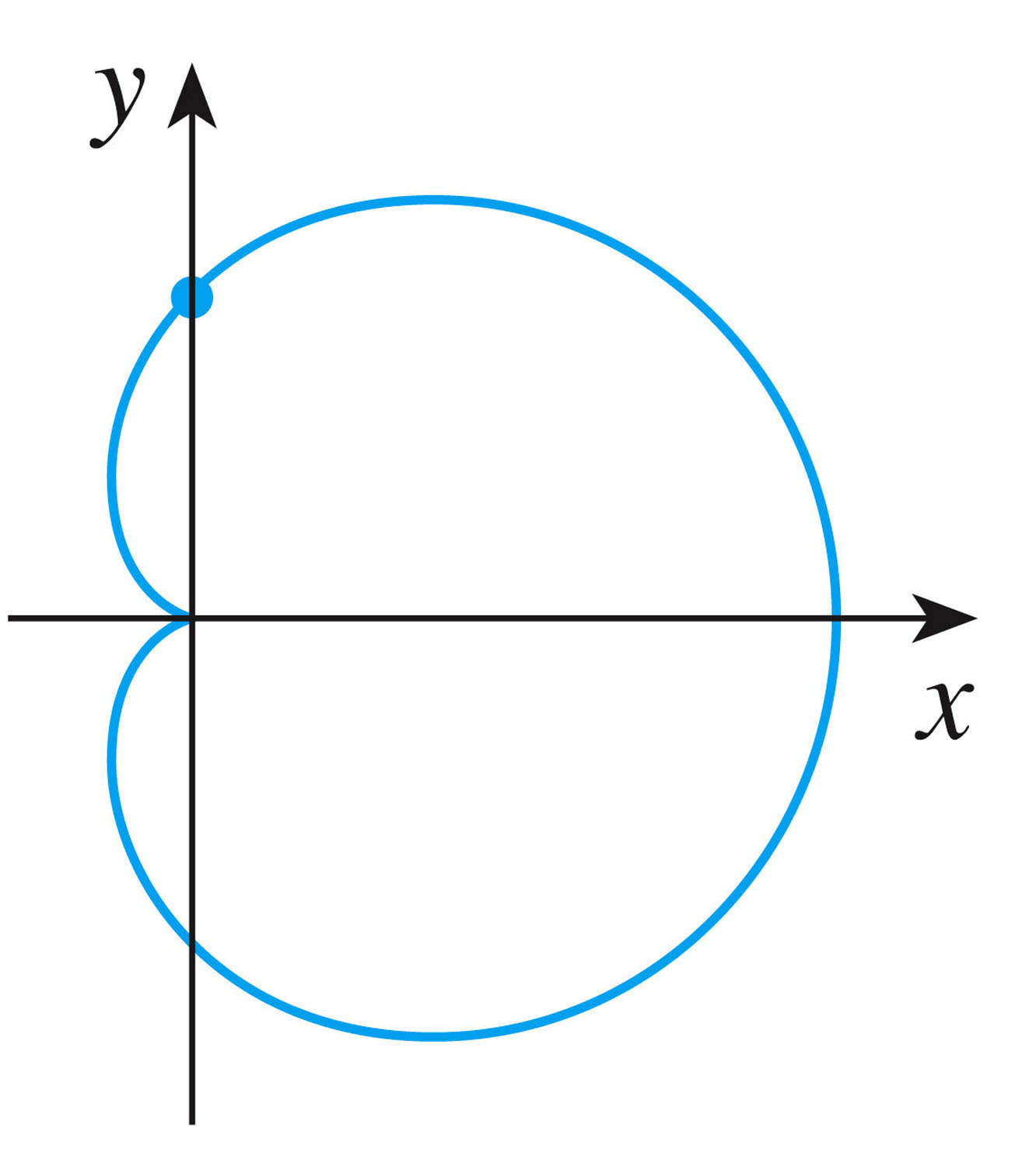
Because the equation is symmetric in $y$ (even in $y$), we expect the curve to be a reflection about the $x$-axis (as it is).
- Let's look at one important application of implicit functions: orthogonal families. #49, p. 163.
- In calculus you encounter the famous ladder problem. Example 2 on
p. 177. We wish to establish the rate of one thing, relative to the
rate of the other. These are so-called "related rates". So the ladder's
top rung is falling vertically at one speed, as the feet are slipping
out at another. Speeds are, in this case, rates of change of positions.
- The problems considered here are the fun ones, the story problems:

- Everyone loves story problems, right?! Let's go over the strategy,
and then try some.
I jokingly use the acronym "UPCE" (oopsie!) for the general problem solving strategy:
- Understand
- Plan
- Carry out
- Evaluate
- Here is our author's more detailed approach to these related rates
problems:
- Read the problem carefully.
- Draw a diagram if possible.
- Introduce (good) notation. Use sensible variable
names. Assign symbols to all quantities that are
functions of time (usually time will be our
independent variable).
- Express the given information and the required rate in
terms of derivatives.
- Write an equation that relates the various quantities of
the problem. If necessary, use the geometry of the situation to
eliminate one of the variables by substitution (as in Example 3).
- Use the Chain Rule to differentiate both sides of the
equation with respect to t.
- Substitute the given information into the resulting
equation and solve for the unknown rate.
- Don't forget your units.
"Warning: a common error is to substitute the given numerical information (for quantities that vary with time) too early." (p. 179). Substitute only after the differentiation is complete.
- Read the problem carefully.
- Examples:
- #4, p. 180
- #6
- #23 (similar triangles)
- #31 (ladders! Pythagoras....)
- #34
- #37 (law of cosines)
- #38 looks like fun....