Day 41, Mat129: Calculus I

Last time

Next time

Today:

Announcements
- You have a quiz at the end of the hour.
- Your homework 4.4 is due.
- Homework 4.5 due Monday.
Today we start by finishing off Section 5.1: the area between curves; then it's into Section 5.2: the volume.
- There's no great shakes here. In our introduction to the integral, we've begun by thinking of a definite integral as representing a signed area, between a curve and the $x$-axis. Now suppose that we want the area between two curves?
  
  If one curve is always above the other, then we simply subtract the smaller area from the larger:
  
  If the top curve is the graph of $f(x)$, and the bottom curve is the graph of $g(x)$, then the difference in the areas, which is what we want (in blue), is
  \[ I=\int_{a}^{b}f(x)dx-\int_{a}^{b}g(x)dx = \int_{a}^{b}(f(x)-g(x))dx \]
  Let's do some examples.
  There are a couple of tricks here:
  1. One is to figure out what to do when two curves cross:
    
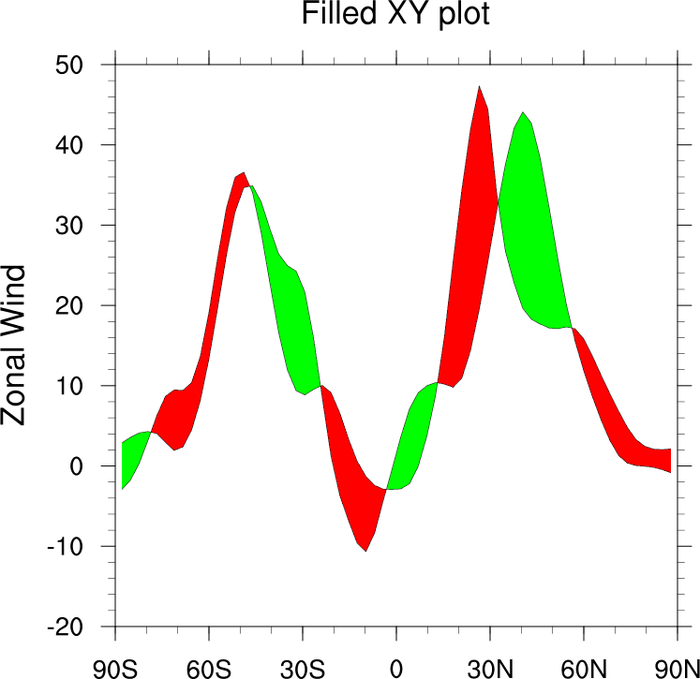
    In this case, the sign of the area changes as $f$ and $g$ change roles (which one is above, which below). If we want the actual geometric area, and not the signed area, then we can use the absolute value:
    \[ I = \int_{a}^{b}|\ f(x)-g(x)\ |\ dx \]
  2. The other trick is integrating along the $y$-axis, rather than along the $x$-axis.
  We'll try examples of both. In every case, think of adding up little chunks of area: \[ A = \int_{a}^{b}dA(x) \] That's a little chunk of area, that we'll write as an infinitesimal rectangle (whose width is $dx$ -- so $dA(x)$ is a function of $x$ -- and whose height generally varies with $x$ as well).
- Examples:
  - #2, p. 349
  - #3
  - #6
  - #17
  - #31
  - #41
  - #45
  - #46
Section 5.2: the volume
- Let's see how to compute volumes of some "simple" (okay, relatively simple!) objects using integrals.
  Before you may have memorized some of these formulas. Now you can derive them! The power of calculus....
  In every case for what follows, we begin with what I consider the most important formula for integral calculus (which in this case we write using the letter $V$, for volume):
  \[ V=\int{dV} \]
  Of course this is also how you would compute integrals of wine ("Vino", adding up little chunks of vino), or even Vemicelli: \[ Vino=\int{dVino} \] or \[ Vermicelli=\int{dVermicelli} \]
  To calculate any quantity $V$, we simply divide it up into infinitesimal quantities $dV$, and add an infinity of them up.
  Now to calculate volumes we'd better know the extent of the object of interest, so we'll march along the $x$-axis from $a$ to $b$, stop at $x$, and add in the little $dV$ that is found there. So in each case what we need to do is find $dV$ (which, by the way, is a function of some other variable, usually -- in the following it's a function of $x$):
  \[ V=\int_{a}^{b}dV(x) \]
  Often (certainly in this section) our next step is to write $dV(x)$ as an area, which is a function of $x$, times dx:
  \[ V=\int_{a}^{b}dV(x)=\int_{a}^{b}A(x)dx \]
  This is the "sliced bread" problem: the volume of a loaf of bread is the sum of the volumes of the slices, which have thickness $\Delta x$ (they're not infinitesimal, because they wouldn't be very filling if they were), and cross sectional area $A(x)$, which varies along the loaf -- like sometimes there's that skinny little heel at the end, with a small $\Delta x$ and a little cross-sectional area).
  
  So our problem becomes to find $A(x)$ -- what are the cross-sectional areas?
  
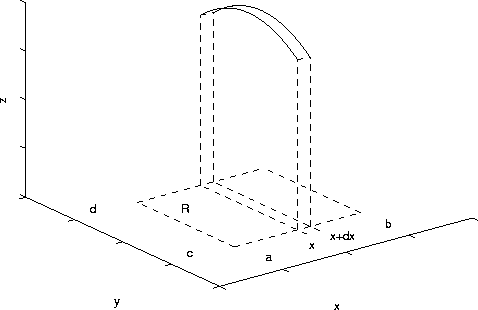
  Let's take a look at some examples:
  - The cube of side length $s$:
    \[ dV(x)=A(x)dx=s^2dx \]
    \[ V=\int_{0}^{s}dV(x)=\int_{0}^{s}s^2dx \]
  - The right circular cylinder of radius $r$ and height $h$
    \[ dV(x)=A(x)dx=\pi{r}^2dx \]
    \[ V=\int_{0}^{h}dV(x)=\int_{0}^{h}\pi{r}^2dx \]
  - The cone of radius $r$ and height $h$:
    \[ dV(x)=A(x)dx=\pi\left(r(1-\frac{x}{h})\right)^2dx=\pi{r^2}(1-\frac{2x}{h}+\frac{x^2}{h^2})dx \]
    \[ V=\int_{0}^{h}dV(x)=\int_{0}^{h}\pi{r^2}(1-\frac{2x}{h}+\frac{x^2}{h^2})dx \]
  - The pyramid of height $h$, and base $s$:
    This is Example 8, p. 359.
  - The sphere of radius $r$:
    \[ dV(x)=A(x)dx=\pi\left(\sqrt{r^2-x^2}\right)^2dx=\pi(r^2-x^2)dx \]
    \[ V=2\int_{0}^{r}dV(x)=2\int_{0}^{r}\pi(r^2-x^2)dx \]
    (the "2" is out in front because we're using symmetry: we calculate the volume of half the sphere in running from 0 to $r$, then double it).
- Surfaces "of revolution" (revolutionary surfaces?) are a special class, and actually a little easier to work with -- because of symmetry. You get cross-sectional areas that are either disks or annuli (rings), so they're defined once you know their radii as a function of $x$: so in this case,
  \[ V=\int_{a}^{b}dV(x)=\int_{a}^{b}A(x)dx=\int_{a}^{b}\pi r(x)^2dx \]
  Let's look at example 2, p. 355.
  Sometimes we "gut" a revolutionary solid with another revolutionary solid, leading to rings:
  Let's look at example 4, p. 356.
  \[ V=\int_{a}^{b}dV(x)=\int_{a}^{b}A(x)dx=\int_{a}^{b}\pi (r_{out}(x)^2-r_{in}(x)^2)dx \]
- Examples:
  - #48, p. 361
  - #4 and 5, p. 360
  - #16
  - #52, p. 361

Website maintained by Andy Long. Comments appreciated.