- Today we'll wrap up that partial fractions problem we
were working on, then move on into Numerical
Integration.
- Next exam: 3/5
- Let's head back into 7.4: Partial fraction
decomposition to finish up that one example.
Will and Natalie are using a slightly different, and very good cross-multiplying approach to writing the equivalent polynomial: \[ \frac{5x-7}{x^2(x+4)} = \frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+4} \] Therefore \[ 5x-7 = x^2(x+4)\left(\frac{A}{x}+\frac{B}{x^2}+\frac{C}{x+4}\right) = \frac{Ax^2(x+4)}{x}+\frac{Bx^2(x+4)}{x^2}+\frac{Cx^2(x+4)}{x+4} \] So, cancelling common terms, we get \[ 0x^2+5x-7 = Ax(x+4)+B(x+4)+Cx^2 = (A+C)x^2+(4A+B)x+4B \] and our three equations \[ \begin{array}{ccccc} {A}&{}&{+C}&{=}&{0}\cr {4A}&{+B}&{}&{=}&{5}\cr {}&{4B}&{}&{=}&{-7} \end{array} \]
- What's integration all about? Well, we usually start by going
about calculating (signed) areas (which means that areas can be
negative):
\[ A=\int{dA} \]
"dA" is called an "infinitesimal" -- it's a tiny chunk of area -- tinier than anything you know ("vanishingly small")!
What's numerical integration all about? We do pretty much the same thing, only we have a finite sum \[ A=\sum{\Delta {A}} \]
where the $\Delta {A}$ are small, but not vanishingly small.
- There are times when we cannot find an explicit anti-derivative function
for an integrand, and hence we are obliged to resort to numerical methods:
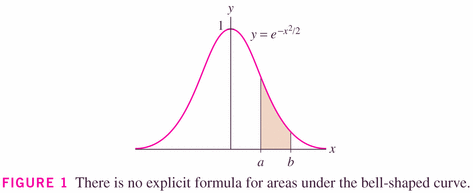
- There are various schemes for numerical integration:
- Left-endpoint Rectangular Rule.
- Right-endpoint Rectangular Rule.
- Midpoint Rule.
- Trapezoidal Rule.
- Simpson's Rule.
- Three of the rules are so called "rectangle rules" (LRR, RRR, Midpoint Rule);
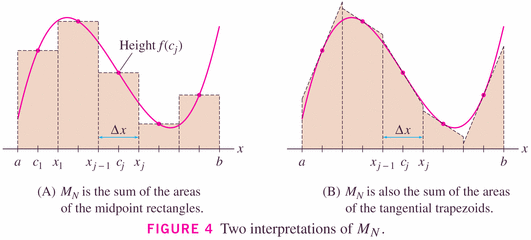
but as the image to the right (above) and the graphical insight below show, we can think of the Midpoint rule as being a "Tangent rule":
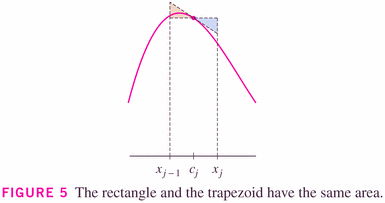
Be careful however not to confuse the midpoint and trapezoidal rule. The trapezoid represented above is not the same as the trapezoid of the trapezoidal rule (which is the average of the left- and right-endpoint methods):
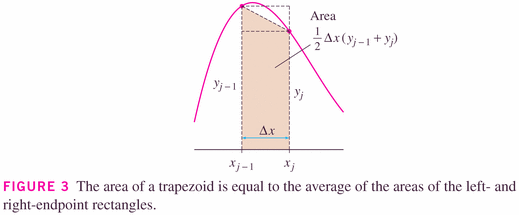
Midpoint Rule: \[ \int_a^b f(x) dx \approx M_n = \Delta x [f(\overline{x_1})+f(\overline{x_2})+\cdots+f(\overline{x_n}) \] where \[ \Delta x = \frac{b-a}{n} \] and $\overline{x_i}=\frac{1}{2}(x_{i-1}+x_i)=$ midpoint of $[x_{i-1},x_i]$.
- The Trapezoidal rule is really just the average of the LRR and RRRs. This gives rise to an important observation, which I want to encourage you to remember, and here it is:
When you have two estimates, you have a third. (their arithmetic average, in this case).
Trapezoidal Rule: \[ \int_a^b f(x) dx \approx T_n = \frac{\Delta x}{2} [f(x_0)+2f(x_1)+2f(x_2)+\cdots++2f(x_{n-1})+f(x_n)] \] where \[ \Delta x = \frac{b-a}{n} \] and $x_i=a + i \Delta x$.
- Simpson's rule is a "blend" (or weighted average) of the Midpoint
and Trapezoidal rules, which perfectly balances the errors of the two
to generate a better rule:
\[
S_{2n}=\frac{2M_{n}+T_{n}}{3}
\]
Notice that the number of subintervals in Simpson's rule must be even.
Now we can go further:
When you have two estimates, you have infinitely many more. (their weighted arithmetic averages).
Here are the error bounds, that illustrate that the errors of midpoint and trapezoidal are related, and suggest how to combine them to create a better method (Simpson's rule):


- Here's a nice summary of the issue, focused on the use of Mathematica to illustrate them. Interesting even if you don't use Mathematica.
- Numerical Integration on-line.
- Here is a hand out which emphasizes this message. Let's take a look at this:
- Mathematica code
- Check midpoint calculation
- Let's do the calculations by the formulas, for
- Trapezoid
- Simpson's
- Check that we get the same things using the averages
- Calculate the true value of the integral, and compare to the approximations. What's surprising?