- Reminder: please keep the phones out of sight and sound.
- I'm returning your reports about the log rule.
One thing I noticed about your addenda is that several groups didn't produce estimates for the half inches. Those were the clearest markings for the 10 foot rule. So I'm still wondering if some of you know exactly how the ruler operates....
- You have an assignment due today: I need you to
evaluate yourselves and your groups for the Dave
project. See the assignment page for
details.
I'd rather that you NOT email me with this info, as emails are public records. I've told you that these are anonymous, but -- officially, at least -- emails may be requested through Freedom of Information requests.
It's harder to obtain paper records!
That's why I asked you to hand them to me.
- Here's my report for
Dave. Please take a look, and ask any questions or
make any comments before I pass it along.
Please read it over, and compare it to your own reports. I intend for these "final reports" to be models which you might follow in your own reports (with a few snarky remarks thrown in sometimes, because these two, in particular, were written for family/friends!:).
If you read the report prior to Sunday, then you missed my structural model for log rules (which we'll discuss soon). It's in the appendix.
- We'll be having our first exam Friday of next week. I'd
like to make the Keeling report due on Wednesday of
next week.
So we'll have finished three projects by then:
- Cross-Country
- Log Ruler
- Keeling
- We finished the $R^2$ derivation. Wow! That took longer than I planned....
Upshot: the variation in the dependent variable, $y$, is split into two parts:
\[ SS_{Total}=SSE+SS_{Reg} \]
and \[ R^2 = \frac{SS_{Reg}}{SS_{Total}} = \frac{SS_{Total}-SSE}{SS_{Total}} = 1-\frac{SSE}{SS_{Total}} \]
which we think of as the proportion of the variance explained by the model (versus the proportion of "error").
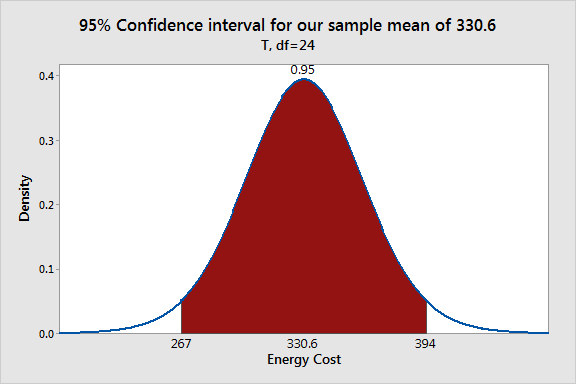
- Let's talk about confidence intervals for parameters: we provide
a box, rather than a single value.
- Often these are expressed in one of two
formats: with 95% confidence,
$a \in [338.07, 340.07]$ or
$a = 339.07 \pm 0.997$ (these were the values of $a$ from the quadratic model to Stewart's Keeling data).
- Confidence intervals are related to p-values, but perhaps
more informative).
- The standard errors of the parameters pop out of the inverse
matrix we compute, multiplied by the mean SSE. Once we have those,
we have everything we need for confidence intervals.
We're often interested to know whether we can exclude a certain value from a confidence interval -- e.g., can we conclude that the slope parameter $b$ in a linear regression $y(x)=a+bx$ is not 0? If so, we conclude that there is a non-zero slope, and the model suggests that $x$ drives values up or down, depending on the sign of $b$.
- Let's check out my discussion of the regressions in the report for
Dave.
$R^2$ is ridiculously high in this case, because we know the function generating the marks on the stick. The errors -- the residuals -- are simply rounding errors, to the nearest board foot. Check out the graphs of data and model....
- Often these are expressed in one of two
formats: with 95% confidence,
- Eventually we may compare models, using statistics
such as anova, AIC, BIC, etc. For now, we're going to focus on
diagnostics pertaining to a single model.
All of these pop out of the model we obtain via linear algebra. - For our next trick(s), we want to talk about transformations of the
data that permit us to continue using linear regression. We've already
seen one:
- if
one does a log-log transformation of both $x$ and $y$, and the data
look linear, then you'll be expecting a power model: $y=\alpha x^\beta$.
(Riegel's model)
- If you log-transform only the $y$, and get a linear looking cloud,
then you'll be looking for an exponential model: $y=\alpha e^{b x}$.
(I've asked you for an exponential model for CO2. You log-transform the trend data, and plot. Then linear regress, if appropriate.)
- What about the oscillations in Keeling's model? We typically model those with sinusoidal functions. Let's write out the model and see what we need to do.... Hint: \[ \sin[2\pi\frac{t-t_0}{T}] \]
- if
one does a log-log transformation of both $x$ and $y$, and the data
look linear, then you'll be expecting a power model: $y=\alpha x^\beta$.
- "The
IPCC stands by its equation of 450 ppm = 2 degrees C [of
warming]....": For years scientists have said that if
atmospheric levels of carbon dioxide reach 450 parts per million (ppm)
the planet would heat up by an average of 2 degrees Celsius above
pre-industrial levels. They have also said that if the world crosses
that threshold, ecosystems worldwide would suffer serious damage.
[ael: by the way -- ecosystems worldwide are already suffering serious damage.... The world won't "suddenly heat up" if we reach 450 ppm -- it's heating up right now, and we're seeing bumblebees struggle with the heat, for example. They pollinate our food -- think about it....]