- Your revised Keeling reports are due Friday. I'm returning
your first reports, which will provide you some specific guidance.
- I'm also giving you have a computational homework due
Friday, as well. Half is related to Keeling, so that's
convenient (a non-linear fit to Keeling's data);
the other half is just a few calculations with Newton's
method. You could do this by hand with a calculator and
our notes from class.
- Some pictures of Wood County weather/climate:
- Perrysburg, OH (Wood County) temperatures
- USA.com weather for Perrysburg
- From NOAA
- I couldn't find Perrysburg normals from NOAA, but here they are
for Bowling Green (about 15 minutes away):
- Bowling Green climate normals
- documentation
- About these climate normals
- Cite this data as: Anthony Arguez, Imke Durre, Scott Applequist, Mike Squires, Russell Vose, Xungang Yin, and Rocky Bilotta (2010). NOAA's U.S. Climate Normals (1981-2010). [Bowling Green, Ohio climate normals]. NOAA National Centers for Environmental Information. DOI:10.7289/V5PN93JP [March 1, 2020].
- I'm still compiling the Fletcher data final dataset, but I want to
illustrate some really good work on data entry.
We still need to reconcile this, but this group appears to be doing exactly what we need to do with data entry.
- Last time we began considering an "unusual" (and I hope
interesting) modeling problem: time to rigor mortis
of cadavers. A little dark, I know -- but the data fitting
is so cool!
-
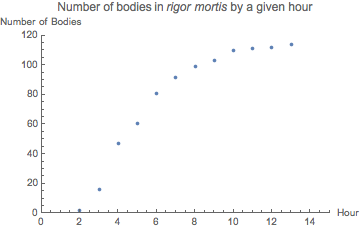
The data is the number of bodies in rigor mortis from two hours on: {2, 14, 31, 14, 20, 11, 7, 4, 7, 1, 1, 2}.
-
- Today:
-
In the course of that modeling exercise you'll see that we can
perform non-linear regression by iteratively solving linear
problems, to approximate a solution to the non-linear
problem.
I'll try to show how this is a generalization of Newton's method.
- Once we take care of that, we'll take a look at some corn seedling
growth data, and weight in grams against age in weeks (use this Mathematica
file). The age goes to 20 weeks, so these are corn stalks
by the time 20 weeks rolls around.
We can see the weight asymptoting by week 20. It's clearly NOT appropriate to model this with an exponential, as John Alexander curiously suggests in Curve Fitting via the Criterion of Least Squares (see Figure 12, p. 23).
- So a logistic curve seems appropriate (more on that in a
moment). But, if we do that, we can actually say more:
we can use the logistic regression to propose an ordinary
differential growth equation for corn.
So the regression serves the purpose of providing parameters for a general (differential equation) model for corn seedling growth. This is an example of a structural model: we tie an empirical model into a structural model, and learn something (or incorporate something) about the nature of plant growth.
This is not "typical", in some sense, of logistic growth. For example, "carrying capacity" is the wrong terminology: and the initial value is never greater than the "carrying capacity" -- the corn seedling doesn't start out monstrous, and then shrivel to a stalk...:)
This model is appropriate if the growth in the weight of the seedling is proportional to its weight, and proportional to a substrate which is ultimately exhausted, and itself proportional to $(K-w(t))$. So "carrying capacity" in this case is sort of the maximal size of the plant that the soil can support.
Plants are notorius for having "switches", however -- at some point they switch from producing leaves to producing flowers to producing fruit.... Lots of ugly non-linearities.
-
In the course of that modeling exercise you'll see that we can
perform non-linear regression by iteratively solving linear
problems, to approximate a solution to the non-linear
problem.
- The history of fracking.
- Study: Fracking prompts global spike in atmospheric methane: "If we can stop pouring methane into the atmosphere, it will dissipate", he said. "It goes away pretty quickly, compared to carbon dioxide. It's the low-hanging fruit to slow global warming."
- The Fracking Industry's Methane Problem Is a Climate Problem (shows some of the methane leak impacts of fracking).
- Robert W. Howarth lecture (12/14/2019) on methane, fracking, and climate change: "Professor of Ecology & Environmental Biology at Cornell University, asking "Is Shale Gas a Major Driver of Recent Increases in Global Atmospheric Methane?" Howarth, who participated in the 2015 Paris Climate Agreement, among other things, is a world authority on the effects of human activity on the environment." He addresses the question of the shape of the methane curve at 1 hour, 5 minutes or so.
- "The
IPCC stands by its equation of 450 ppm = 2 degrees C [of
warming]....": For years scientists have said that if
atmospheric levels of carbon dioxide reach 450 parts per million (ppm)
the planet would heat up by an average of 2 degrees Celsius above
pre-industrial levels. They have also said that if the world crosses
that threshold, ecosystems worldwide would suffer serious damage.
[ael: by the way -- ecosystems worldwide are already suffering serious damage.... The world won't "suddenly heat up" if we reach 450 ppm -- it's heating up right now, and we're seeing bumblebees struggle with the heat, for example. They pollinate our food -- think about it....]