Day 02, MAT115

• Announcements:
  • All but 10 of you have introduced yourselves on Canvas. I'd like 100% of you to do so! Please introduce yourself if you haven't yet (and you might go back and meet some more. You're an interesting group!

  • I've had several people email regarding the logo. The logo is due at the end of the course, after you've learned a whole bunch of cool math. So be patient for that!

    But keep your eye out for math that resonates with you, and be thinking about what you might like to incorporate into your "family crest".

  • There are three videos covering the material today (walking you through this page):
    1. YangHui's Triangle
    2. The Great Fraudini Trick
    3. Wrap Up

• Last time we set off in the pursuit of an understanding of an ancient Chinese artifact (circa 1300 AD), and you all some wonderful guesses, conjectures, and hints on the Canvas discussion page. Thank you so much for your contributions!

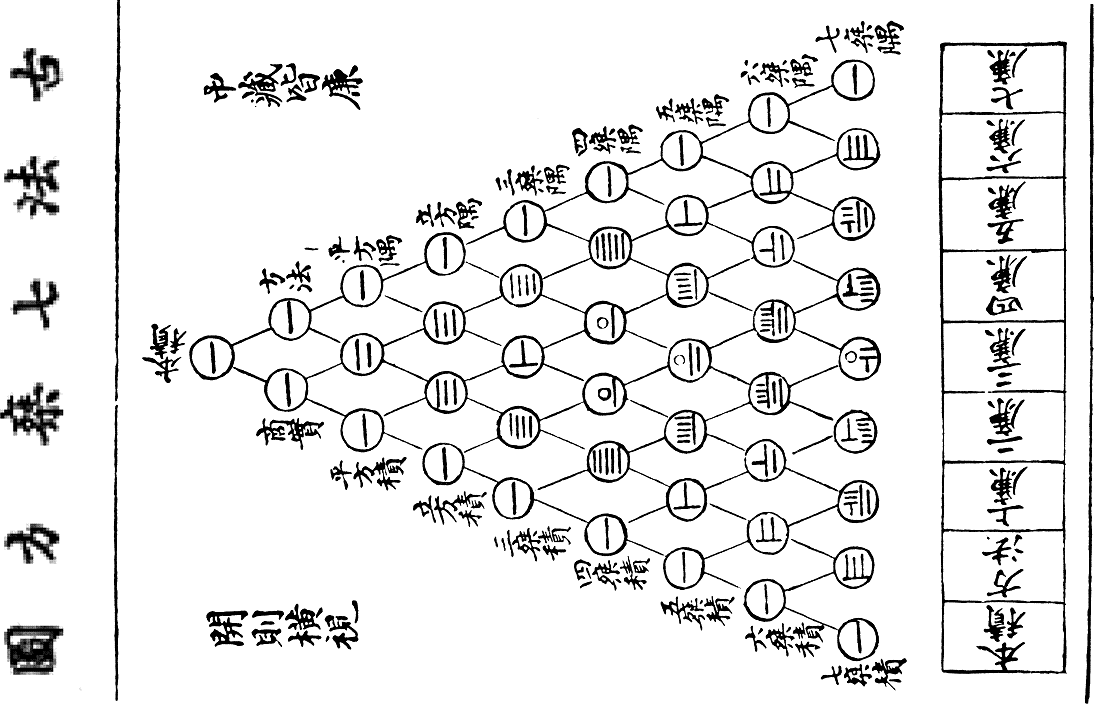
  I hate to spoil the surprise by telling you exactly what it is -- many of you seem to have figured it out, and found the error in the chart.

  Here are some key words and ideas, however:

  1. Symmetry -- the triangle is symmetric (which is one way of discovering the location of the error, by the way).
  2. Exponential growth -- We hear a lot about things growing "exponentially" these days -- mostly Covid numbers...:( -- however this has a technical definition in math; and, indeed, this artifact shows signs of it!
  3. Addition, of two numbers to make a third
  4. "repeated" -- do it again, do it again....
  5. Persistence: "The longer I look at this chart, the more I understand it."
  6. Looking at things from a different perspective (literally!): "it started to make more sense when I flipped it on its side."
     

  7. Restriction: try to figure it out using just the first few rows (restricting you attention helps you to see more clearly).
  8. Generalization: "consider a family tree"
  Katia gave a hint, saying that "it could be an arrangement of numbers in old Chinese symbols".

  Let's suppose it is. If we can figure out the number pattern, then we may be able to figure out how the "old Chinese symbols" work! We can use the mathematics to help us decipher a system of writing.

  If you're an anthropology major, you may suddenly see the value in knowing a little mathematics...:)

  If you know the mathematics, can you write the next row in the series, in both our numbers and in the writing of the Chinese scribe?

  Many of you mentioned "sequence" -- it turns out that there are all kinds of numerical sequences represented in this table, and we'll study several of them. For example, I would wager that many of you noticed a sequence of repeating ones (along the two side diagonals).

  Evan mentioned "a sequence found in nature" -- it turns out that one of nature's favorite sequences is concealed in this triangle. We will study it further on down the road.

  But it's not a Chinese Christmas tree, Susan -- sorry to pass that sad news along to your third grader! Good idea to show things to kids, however: their brains are very flexible.

  So: if it's not a Chinese Christmas tree, then what is it? Well, if you put it all together, you get a thing called "Pascal's triangle" -- let's take a look at that now.

  
  • Different kinds of numbers appear in diagonals, which we should all be able to identify:
    • a line of 1s
    • the counting numbers: 1, 2, 3, 4, ....
    • The diagonals can be thought of as "accumulators": and McKenna suggests a pattern for them: "...in each row the 1st and 2nd symbols are added to create the new symbol in the middle of the row beneath it. This is repeated in each row."

    So let's do that, using this hexagonal paper (it just makes life easier). Next in line are some less familiar numbers:
    • triangular numbers:
      

    • tetrahedral numbers:
      

  Counting is a critical step in probability, and the Pascal in "Pascal's Triangle" is Blaise Pascal (1623-1662), who studied it to help him compute probabilities:

  

  The triangle was known long before Pascal, however: for example, YangHui's triangle is the 13th century Chinese version of our triangle; but that's not the oldest known version (the Indians probably knew of triangle as early as several hundred years BC).

  One thing that Pascal's triangle allows us to do: it allows us to understand how this Chinese culture of the 13th century wrote its numbers (Chinese Bamboo Counting Rods). How did these people write 15? 28? 30?

• Haven't given away the mistake that the scribe made -- can you find it now?

  ---

• We've been talking about different kinds of numbers, but now let's talk a bit about the concept of "number" itself. For that, one turns naturally to Sesame Street!

  I asked you to do the reading "From Fish to Infinity" for today, in which we learn the answer to one of life's persistent questions:

  What is "six"?

  We learn something of that, anyway -- at least about six fish. But

  "Six is more ethereal than six fish.... It applies to six of anything..., the ineffable thing they all have in common." (Joy of X, p. 4)

  We learn that

  • "...numbers are shortcuts for counting by ones...." (p. 5)
  • Furthermore, "...Humphrey might realize he can keep counting forever." (p. 5) -- something that will be very important when we come to talk about infinity.

  Did you notice Humphrey using any other cues to help him keep track of the number of fish?

  This leads us to your next reading: Rock Groups

  fish fish fish
  fish fish fish
  

• Having visited with the Chinese, we will soon turn to the Egyptians. They will be tied up with some of the numbers found in Pascal's triangle. Before we go there, however, how about a little "Fun and Game" to begin: a visit from my close friend, the Great Fraudini!

  It turns out that the Great Fraudini can read anyone's mind -- so long as they're thinking of a number between 1 and 63, and they're willing to play a little card game with me. So let's see how this works....

  • Rules of the game: you show the chump every card. If they see their number on it, they say "Yes"; otherwise they say "No". Then you tell them their number!
  • Can you win at the game? (You should be able to do it every time!)
  • Here's the handout for the cards, if you want to print off a copy. You need a set of cards to play!

  So it turns out that the key can be found in Pascal's triangle! It seems that just about everything can be found there....

• FYI: It turns out that I'm a really bad magician -- because I always give away my tricks!:) But I want you to be able to perform the trick, so I'm not giving it away -- I'm paid by your tuition dollars to do this, so you should get something back.

  So in case you don't have a magic trick up your sleeve, I'm giving you one!

  However I want you to think about it before I just give it away. Turn to your Fraudini discussion page on Canvas to make some conjectures, and guesses as to how I am (or rather how that Great Fraudini is) able to perform this magnificent trick!

  (And try it out on some third graders, if you can! Let them figure it out....)

• I always tell my students in MAT115 that my real course objective is to help my students make money by gambling. I'm going to teach you some tricks that might win you a drink somewhere, somehow....

  By the way, I always tell my students in MAT115 that gambling is foolish, unless you have inside information. So I'm all about giving you the inside information. But generally, and (in particular): "a lottery is a tax on people who are bad at math."

fish fish fish
fish fish fish