- Last week was our introduction to each other, to Number games, and
to Pascal's triangle.
- Last "class" you met up with The Great Fraudini, who is able to
read minds!
This magic trick, carried out with the help of six simple cards, no doubt amazed and astonished you, and made you think "Hmmm... maybe there's money to be made here!"
Today I will share the secret of the Fraudini ("Bad magician! Never give away your secrets!"); but I want you to be able to astonish and amaze all your friends and kids and nieces and nephews, too.
- Of course there will be something new, too. A deeper understanding
of Pascal's triangle; and a look at how primitive cultures may have
counted their sheep....
- There is just one video covering the material today (walking you through this page), but boy
 |
 |
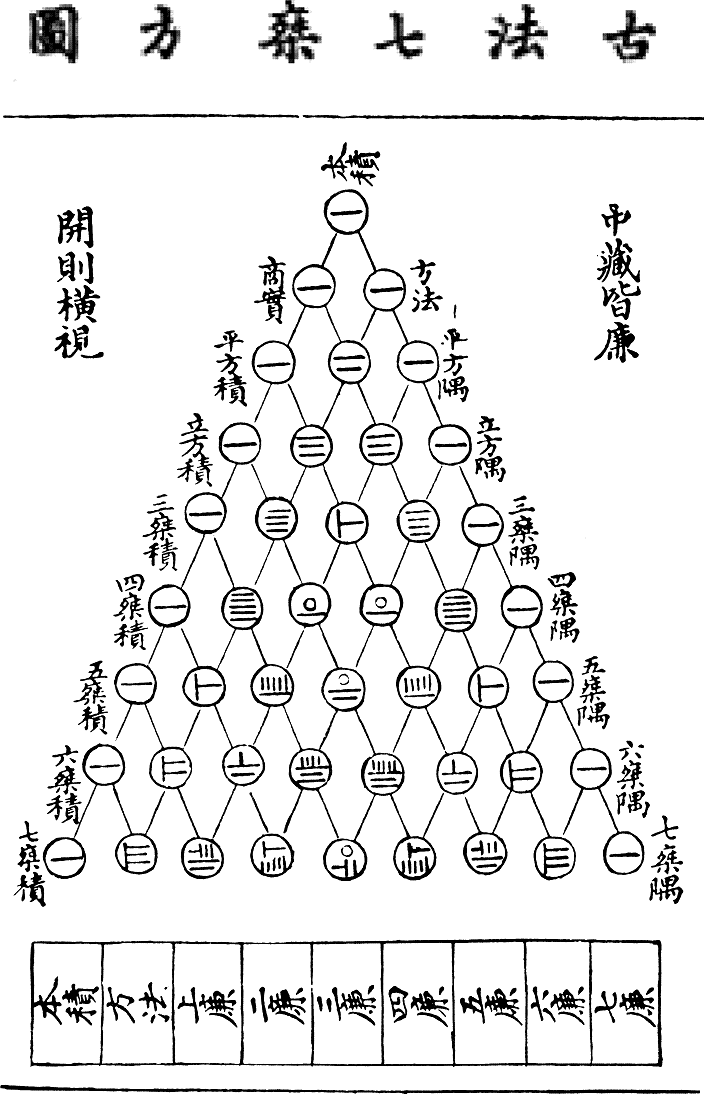
(aka Pascal's triangle).
I also showed you how one builds Pascal's triangle; and we talked about some of the numbers found therein (e.g. counting numbers -- also called the natural numbers, 1, 2, 3, and so on; triangular numbers; tetrahedral numbers; etc.)
Some of you were able to use your amazing powers to figure out the secret (including, I think, the amazing power of google...:). Here were some really important and interesting observations from the discussion:
- All cards end with 63 (and Alex noted that "If they say yes to all cards, it has to be 63." In other words, 63 is the only number on each of the cards. So that's an easy one for Fraudini, for sure.).
- Each card has half the numbers on it.
- Cards start (upper-left corner) with 1, 2, 4, 8, 16, 32.
- Becky observed that "On each card, the second number becomes the
the gap between some of the numbers after...example... Card starting
with 16 17.....it gets all the way to 31, the skips to 48...17
spots. Card starting with 8 9...it gets to 15, skips to 24....9
spots....then 31 to 40...and so on. They are all this way except the
card with all of the high numbers starting
with 32." And Becky ended with a plaintive cry, of "Why Fraudini
why!?!"
(Yes, mathematics can be painful. But we hear your cries, and will try to heal your math wounds!)
Meanwhile, Becky will be the first to tell you that, now that she's figured it out, she's been torturing her son by reading his mind....:)
- Emily had a great comment: "Whether or not he said no or yes to
the first card automatically eliminates say about half the numbers,
same to the next one, and so on and so forth. So the first number is,
for example, 15. The person says no to the first card, let's say all
the evens. That gives us 32 numbers left. The next card is only numbers
that end in 1 or 3. The volunteer doesn't see their number on that
card, so that only 18 numbers. The next could be numbers ending in 5,
they say yes, and then there is only 6 numbers left. The next is
numbers 5-25, that card eliminates all but 5, 15, and 25. Then its
numbers divisible by three, and that leaves 15."
This is, in effect, exactly how the trick works. But I (oh, sorry -- I mean The Great Fraudini) couldn't be bothered to work that hard, being a lazy mathematician.
But the idea of the process of elimination is great. I just need to know one number on each card to tell what's been eliminated (an example from Emily's remarks is this: "all the evens" -- I can eliminate the card known as 1.)
- Savannah lays it out, in the end: "For example, the number 17 only
appears on two cards, one with the number 16 in the top left hand
corner and one with the number 1 in the top left hand corner, and that
adds up to 17. I believe this is how Great Fraudini was able to figure
out the number that was chosen."
And that's exactly right:
- Each card is known by its upper-left-hand number.
- Add up the "Yes" cards, and you know the number in your friend's mind.
- Now I ask this: "Why does it works?"
The secret of Fraudini's trick is this secret of the counting numbers, 1, 2, 3, 4, ....:
Every counting number is either a power of 2, or can be written as a sum of distinct powers of 2 in exactly one way.
Here are the first few powers of 2:
\[ \begin{array}{c} 2^0 = 1 \cr 2^1 = 2 \cr 2^2 = 4 \cr 2^3 = 8 \cr 2^4 = 16 \cr 2^5 = 32 \cr 2^6 = 64 \end{array} \]
- By the way, one student last week suggested that the triangle
illustrates "exponential growth". Powers are what exponential growth is
all about. If you double something (as we're doing here, starting from
1), you multiply by 2; and if you double 1 say every week for 20 weeks,
you get to
\[
2^{20}=1048576
\]
Over a million. So ask your friend if he or she can double their number
of push-ups every week for a couple of months, and see how they do!
This is exponential growth -- the real thing.
- The fact that there is a unique way -- exactly one way --
to write a counting number is the secret to Fraudini's trick. This
trick is more properly called the "Binary Card Trick", because what
we're really doing is using "binary" numbers (base 2) to represent the
numbers we usually think of in base 10.
So in base 10 we think of "17" as \[ 17 = 1*10 + 7*1 = 1*10^1 + 7*10^0 \]
Savannah says that $17=16+1=2^4+2^0$. Try to write 17 as a sum of distinct powers of 2 in another way. (Good luck! You can't.) You can write \[ 17=1+8+8=2^0+2^3+2^3 \] -- but those aren't distinct powers of two. So the "distinct" part is really important.
So 17 appears only on the 1 card and on the 16 card. We figure out how to write a number as a sum of powers of 2, and then we write that number on each of those cards. And then it will be the only number exclusively on those cards -- and the sum will tell me the number!
-
Fraudini used his amazing powers (his amazing powers of 2, that is) --
to "read peoples' minds!" I hope that you make a buck or two reading
minds this weekend....
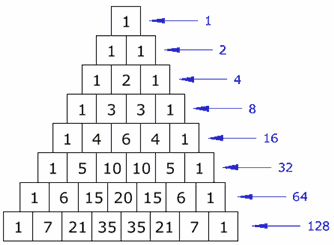
It seems like everything is in Pascal's triangle! (We'll find more interesting numbers!)
But how might "primitive" people have counted? (We'll use a mathematical concept called a "tree" (a type of graph) to help us. More on those later....)
There are at least three good suggestions that I know of:
- Tallies
(your next assigned reading talks more about tallies).
- One-to-one correspondence
- using body parts -- "one hand" of sheep, say -- meaning five sheep.
- cairns:

- And then an unusual method of "counting by partitions" that
Patricia Baggett and Andrzej Ehrenfeucht proposed at the 2011
National Math Meetings.
- They proposed that primitive societies may have counted
this way. Let's suppose you need to let the King know how many
sheep you have (but you were never taught how to count):
- divide your sheep equally ("one for you, one for me") into two pens: either there is one left over, or not. You make a note of whether there is one left over or not.
- Send all the sheep in pen two (and any "left over") out to pasture, and then
- You divide the sheep in pen one into pens one and two: i.e., just do it again! And again, and again, and.... until you get down to a pen one with just sheep in it.
- Now let's see how we might record the results to send to
the King.
The easiest way to illustrate the counting method is via a tree.
Let's see how we might use a tree to represent the solution to the "22" counting problem: in the linked example, we would get 10110 by writing the remainders from left-to-right starting from the bottom of the tree. (The result should always start with a 1 if done correctly, since we always end with one sheep!)

The answer will be written as 1, 0, 1, 1, 0
That is, from the bottom up, left to right. This is important! We have to have a consistent scheme for writing.
So how do we write
- 9 sheep
- 31 sheep
- 54 sheep
- Can you go backwards? How many sheep is meant by
- 1,1,0,1,1,0,0
- 1,1,0,1,1,0,0
- 1,0,0,1,0,1,1,0,1
Try making a tree with these remainders.
- They proposed that primitive societies may have counted
this way. Let's suppose you need to let the King know how many
sheep you have (but you were never taught how to count):
We want to understand each of these notions:
- prime,
- composite,
- square, and
- triangular numbers
So we're interested in arranging our pennies (i.e. rocks) in groups with certain properties.
All numbers of pennies can be arranged into a line (this is Humphrey's "Furry Arms" method):





Some numbers of pennies can be arranged into
- rectangles (of more than one row):

Note that this is how Humphrey said the number of fish -- he blocked the fish into two groups of three fish --
fish fish fish,
fish fish fish - You'll know why squares are special if you make
some with pennies: 1, 4, 9, 16, and so on.
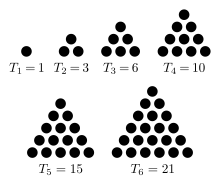
- triangles lead to "triangular numbers" that we saw in
Pascal's triangle last time:
Another way of saying that a number is composite is to say that it can be broken up into groups (each with more than one member) that can each be put into one-to-one correspondence with each other (that is, each element in one group has a partner in another -- and just one partner. Perfect for a dance....).
So 9 is an example, a square. It can be broken into three groups of three; so each group of three can be put into one-to-one correspondence with any other group of three.
Notice that we said greater than one in the definition above. The number 1 is special, and considered neither prime nor composite.
We've already heard this important rule, which you learned at some point in your mathematical education:
Every natural number (other than 1) is either prime, or can be expressed as a product of primes in exactly one way.
Let's look at examples of each.
- Using your pennies, make (and document) all rectangles for pennies up to 15. Then answer me this: "What's special about 12?"
- Find and illustrate the triangular numbers until you run out of pennies!
- odd and even
- odd and odd
- even and even
| + | Odd | Even |
| Odd | ||
| Even |
Rock groups suggest formulas for representing even and odd numbers:
| Evens: | 2*n |
| Odds: | 2*n+1 |
It might be better to write them this way:
| Evens: | 2*n+0 |
| Odds: | 2*n+1 |
Start with a number, like 22, and start dividing it up into two equal groups (if you can -- i.e., if it's even -- with 0 left over) or two equal groups with 1 left over (if it's odd). And do it again, and again, and again, until done: \[ \begin{array}{l} {22=2*11+0}\cr {22=2*(2*5+1)+0}\cr {22=2*(2*(2*2+1)+1)+0}\cr {22=2*(2*(2*(2*1+0)+1)+1)+0}\cr {22=1*2^4+0*2^3+1*2^2+1*2^1+0*2^0}\cr {22=1*16+0*8+1*4+1*2+0*1} \end{array} \] (starting from $2^4$ because there are four 2s out front).
Do you see where this result comes from? Everything after all those twos, 1+0)+1)+1)+0, turns into the multipliers for the powers of 2: gets turned into \[ 22 = {\bf{1}}*2^4+{\bf{0}}*2^3+{\bf{1}}*2^2+{\bf{1}}*2^1+{\bf{0}}*2^0 \]
And if you show someone thinking about the number 22 your Fraudini cards, they'll pick out three cards: the 16 ($2^4$) card, the 4 ($2^2$) card, and the 2 ($2^1$) card: $16 + 4 + 2 = 22$.
- how Fraudini's trick works;
- how composite numbers differ from prime numbers;
- how primitive counting works;
- and how primitive counting is related to the binary card trick.