Day 04, MAT115

• Overview/Babylon
• Babylonian Number Examples

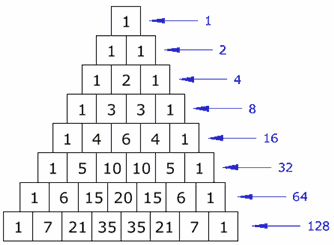
The six simple cards each represent a power of two, and we discovered that there's only one way to represent a counting number as a sum of distinct powers of two.

So once your "opponent" points to the cards which contain their number, you just add up the cards, and you tell them their number. Magic! Not....

We talked about some possible counting strategies:

• One-to-one correspondence
  • Tallies:
    

  • using body parts -- "one hand" of sheep, say -- meaning five sheep.
  • cairns: 'An old Scottish Gaelic blessing is "Cuiridh mi clach air do charn, "I'll put a stone on your cairn." In Highland folklore it is believed that the Highland Clans, before they fought in a battle, each man would place a stone in a pile. Those who survived the battle returned and removed a stone from the pile. The stones that remained were built into a cairn to honour the dead.

• And then an unusual method of "counting by partitions" that Patricia Baggett and Andrzej Ehrenfeucht proposed at the 2011 National Math Meetings.

  They proposed that primitive societies may have counted this way. Let's suppose you need to let the King know how many sheep you have:

  1. divide your sheep equally ("one for you, one for me") into two pens: either there is one left over, or not. You make a note of whether there is one left over or not.
  2. Send all the sheep in pen two (and any "left over") out to pasture, and then
  3. You divide the sheep in pen one into pens one and two: i.e., just do it again! And again, and again, and.... until you get down to a pen one with just sheep in it.
  4. Record the results to send to the King. (So how do we do that? Maybe string and knots?)

• We have also learned a few lessons from Sesame Street:

  • One-to-one correspondence with the "counting numbers" (we'll call them the natural numbers -- 1, 2, 3, 4, 5, ....).

    The essence of "fiveness", say, is that you can take your favorite set of five things -- say the fingers on a hand -- and if you can match them up exactly with another set of things (e.g. the toes on one foot) -- each one with a unique partner -- then you know that you have exactly five toes, too.

    All the counting numbers up to a certain number (e.g. five) is a particularly good set of favorite things. So when we say the numbers "{1,2,3,4,5}" in order, we are thinking of that as "fiveness", and we are partnering up our fingers or toes with "five", to say we have five fingers or toes.

    The process of counting is the process of partnering, and creating the "one-to-one" mapping.

    (This might seem entirely obvious for "five", but wait until we get to "infinity"! Then you'll be glad that you understand the one-to-one mapping!)

  • Prime Factorization -- 6=2*3=3*2

    You've no doubt known for a long time that there are prime numbers and composite numbers, but you may not have thought of the prime numbers as those you have to represent as rocks in a line, and composite numbers as those whose rocks you can put into more interesting rectangles.

  • "Blocking" numbers helps us to get the count: fish, fish, fish
    fish, fish, fish

    Yesterday I was telling my wife how to spell "snopes" (she was going to check and see if, in fact, the Bernie Inauguration Meme is really available on a sweatshirt), and I told her to go to "snopes". She said "how do you spell snopes?", and I said

    s,n,o
    p,e,s

    and I realized that I'd blocked it to make it easier for her to get the spelling.

Here are a few of my musings:

1. How cumbersome are the Roman numerals! How would you write your own birth year? (Mine is MCMLXI -- now you know how old I am!)

2. "biology is deeply embedded" in number systems (10 "digits" in our system; tallies of 5; 5 and 10 in Roman numerals, and then multiples of 5 and 10; 10 in Babylonian; 5 and 20 for the Mayans)

3. Babylonians based their system on -- its prime factorization gives it lots of factors. Our author Strogatz calls 60 "an exceptionally pleasant number." I hope that you agree!

4. We need no new symbol for 10 in our Hindu-Arabic numerals: we use only the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 -- and place value (hence the name of the chapter: "location, location, location").

5. Place value suddenly makes arithmetic possible. "Just master a few facts", our author says.

   My own musing: it's interesting that we seem to be abdicating our arithmetic to machines, and imply that it's not important to do arithmetic anymore. I would say that basic numeracy is tremendously important -- but oftentimes, more important than the exact answer is a good estimate. We could work harder to develop that skill.

6. The frequenly unsung hero of the Hindu-Arabic numbers is the digit 0 -- a symbol for nothing! (The Babylonians can't distinguish the numbers 1 from 60, without some additional context -- as we'll see today!)

   Well let it be unsung no more! I hope that you'll enjoy this rendition of

   Zero, My Hero

7. Binary, or base 2 math: a place-value system with just two symbols, 0 and 1. Perfect for computers, for Binary Card Tricks, and for primitive counting!

8. Cornell built the first telegraph line (Baltimore to Washington, D.C.): 1844. I know that the telegraph displaced the pony express, which only ran for one year, at the beginning of the Civil War (1860-1861).

• Babylon, then (source)
  

• Babylon, today

• I want to introduce you to their mathematics via a "detective story": I hope that you all like detective stories.... The story is called Sherlock Holmes in Babylon.

  Today we're going to play Sherlock Holmes, and solve a mystery.

  The author, Prof. Buck, guesses that the document comes from the city of Nippur, in what is now Iraq:

  

• the Babylonians and place value?
• the purpose of the table?
• the Babylonian's missing number(s)?
• the way Babylonians looked at numbers and their world?
• the Babylonian influence in our world today?

How would the Babylonians write these numbers:

1. 47
2. 573
3. 3600
4. 14001