- Last time we encountered the Hilbert Hotel. We continue with that
today, as we end our course on an infinite note.
- First of all, your logos are due this Thursday by midnight. Here's
what was said in our syllabus:
LOGO: Companies have logos; you should have one, too! Your math logo will be something (like a family crest) that represents you. It will be created using elements from this course (or other mathematical elements of your own choosing). You will type up a one-page sheet, illustrating and explaining your choice. These will be exhibited on-line.
Over the weekend I was in Anderson Township, and I saw this logo on a dumpster: do you see the cinquefoil knot?

So I'll have you submit to me your logo and a one-page paper as an assignment, and then I'll have you put your logo and a description (you could just copy the text from your paper) onto a discussion board, so that everyone may enjoy them.
It will be a digital poster session, essentially.
This is your last assignment prior to the final.
- Homework(s) recently graded (about which I'll make a few remarks):
- A knotty problem
- Distinguishing Knots (key thanks to Emilys K. and B.) and a video.
- Homework even more recently graded (or being graded):
- Fractal spiral and mirror images: Grading was/is easy: all of you who
submitted both on time receive full credit --
those who were late lose 10% per day.
- Your Fractal homework (and a key):
- The four fractal: here are some iterations, from a starting vertical stick
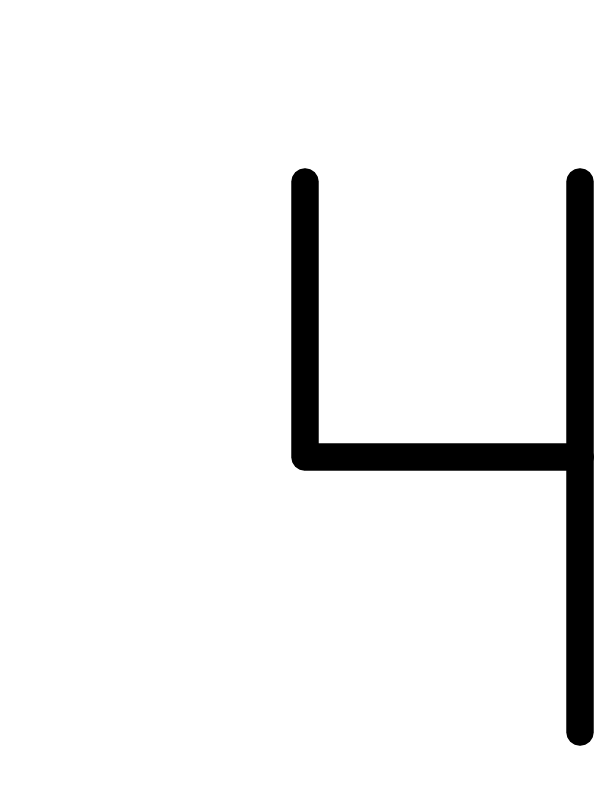
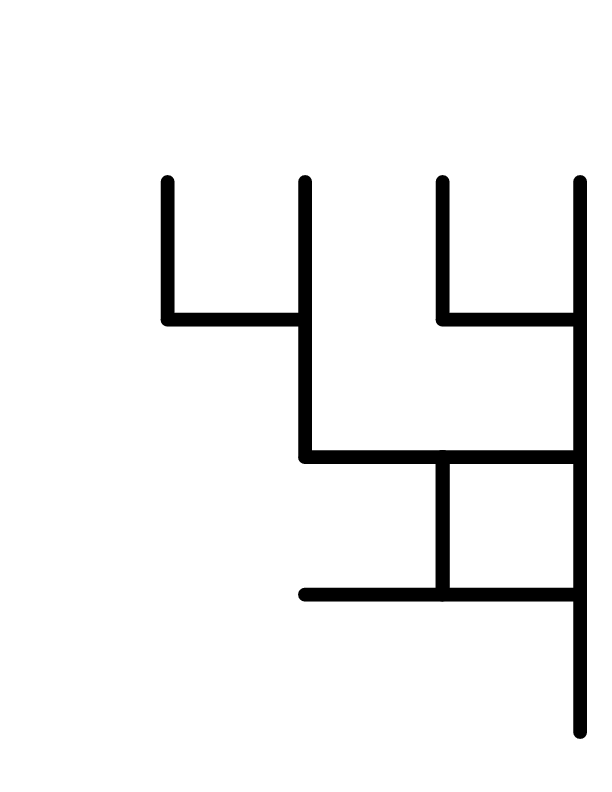
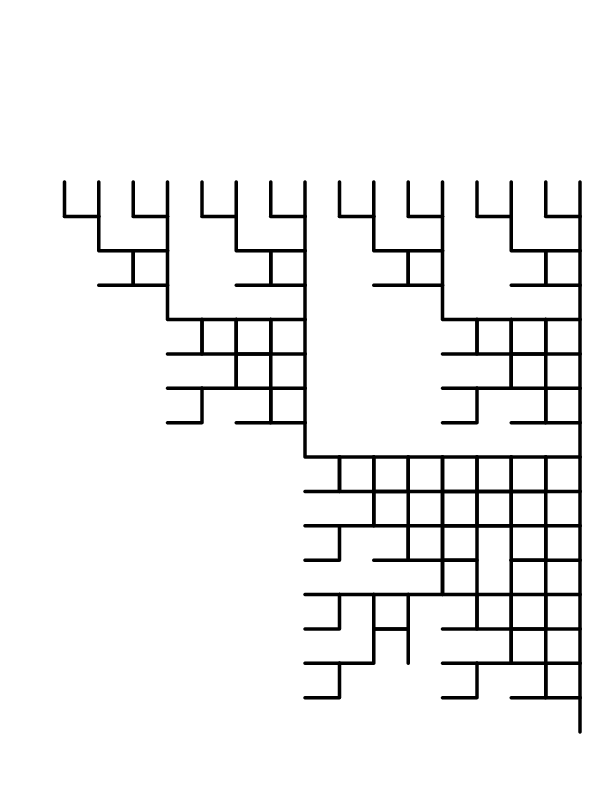

1 iteration 2 iterations 4 iterations 9 iterations The number of sticks is growing exponentially, by a factor of four: $4^n$ at the $n^{th}$ iteration.
The length of the fractal heads off to infinity, even though the fractal lives in a little square.
- Fractals rely on a process whereby an object is
transformed in such a way that more copies of the original
object are produced, upon which one can again perform the
fractal process. So this process takes a white square and
produces more white squares -- then "do it again, do it again!"
The area left quickly goes to zero, as $\frac{4}{9}^n$ for the $n^{th}$ iteration.
- Area and a stick fractal:
- This time a dark square produces dark squares; and the area left quickly goes to zero, as $\frac{4}{9}^n$ for the $n^{th}$ iteration. (Again!)
- For the stick fractal, a stick is broken into 8 1/4-length sub-sticks; since the length is doubling in size at each step ($8*\frac{1}{4}=2$), the length is increasing as $2^n$, and will become infinite if we continue forever.
- The four fractal: here are some iterations, from a starting vertical stick
- Fractal spiral and mirror images: Grading was/is easy: all of you who
submitted both on time receive full credit --
those who were late lose 10% per day.
- Your comprehensive final will be available Tuesday, May 4th, at 8:00 am through
Thursday midnight.
As in previous exams, you will have an IMath component, and a Canvas component (which you should do immediately following your IMath portion).
This Thursday I will do a review of the course, and what you might expect on the final. It will be covering some new material, plus revisit some of the old material previously covered on exams.
If you have particular questions, get them to me by Wednesday night so that I might address them.
- Materials for today:
- Two videos covering today's material: The middle and The end of the Hilbert Hotel
- More Hilbert Hotel scribbles
- We focused on a very strange fact about infinity: that when we get
to sets that are infinitely sized, you find that their subsets
can be exactly the same size as the set itself.
For finite sets this never happens. Since we generally only work with finite sets of things (like your collection of antique cars, or pets, or whatever) it seems very mysterious. And it is!
- The test of the size of two infinite sets is whether they can be
put into one-to-one correspondence. If they cannot be, then
their sizes (cardinalities) are different -- one infinity is "bigger"
than the other.
We used a special hotel, "The Hilbert Hotel", to illustrate this strange fact of infinity.
- Definition: the Power Set of a set is the set of all
subsets; and Pascal's triangle shows you how many of each type
of subset you have (for finite sets).
Even the set containing no elements has one subset -- the set itself. So the power set of the empty set has one element -- has size bigger than the set itself ($1 \gt 0$).
This property holds true for all finite sets -- and it turns out to be true for infinite sets, too!
- This means that, although the set of natural numbers
$\{1,2,3,\ldots\}$ is infinite as a set, there's a bigger
set (the power set of the natural numbers). Upshot:
infinity comes in various sizes!
And, once we've illustrated that, we can conclude that there are infinitely many sizes of infinity, each bigger than the one before....
- If you've done your reading, then you already know that the real
numbers -- numbers including all the natural numbers, plus all
the fractions, plus all the irrational numbers like $\sqrt{2}$
and $\pi$ -- is a set bigger than the set of natural numbers.
There's no way that you, the amazing desk clerk at "The Hilbert Hotel", can make room for everyone when the real-numbered school bus pulls up.
We've seen that you managed to handle a lot of tricky situations:
- The place is packed, and one person shows up;
- The place is packed, and an infinite school bus (with naturally numbered seats) shows up;
- The place is empty, and an infinite number of infinite school buses show up;
- The place is packed, and an infinite number of infinite school buses show up.
- The set of natural numbers $\mathbb{N}$ is the same size as the set $\mathbb{N}$ with any finite number of new elements added to it.
- The set of natural numbers $\mathbb{N}$ is the same size as its subset of evens or odds -- or, in fact, any of its infinite subsets (e.g. the primes); or that the set of natural numbers $\mathbb{N}$ is the same size as the set of all integers ($\mathbb{Z}$ -- including the negative natural numbers, and 0).
- The set of natural numbers $\mathbb{N}$ is the same size as the
rational numbers ($\mathbb{Q}$: all real numbers with
terminating or repeating decimal representations).
The irrational numbers -- denoted $\mathbb{I}$ -- have non-terminating, non-repeating decimal representations.)
- It was Georg Cantor who created this "paradise" (David Hilbert's word) of infinities. Paradoxical things lead some to explore, and I hope that you'll explore with me one corner of this paradise. Let's take a look at two mysterious cases, described in our text (with details on this set of pages).