- Your first exam is upon us. Here's a review.
- Half of your first exam will be on IMath, the other half is
on Lockdown browser. For the first (IMath portion), you may use
any technology (Mathematica, calculator); for the Lockdown
browser part, you may use only the scientific calculator that
comes within the Lockdown browser.
Each is available from 8pm Friday to 8pm Sunday.
- Please (please, please, please, please) reach out to me
if you are struggling in any way.
- I have graded the Week 1 homeworks that arrived by Midnight Thursday. A key will be available on this page on Saturday (since the due date for the assignment is Friday at midnight). I'll continue to grade those as they come in today.
- I want to remind you that there are section
summaries for the sections which we have studied to date, which
contain important formulas and highlights from each of the sections we
cover. If you haven't looked at those yet, you might take a peek.
- I also want to remind you of a few formulas from calc I, which are
especially useful in these first few weeks:
- Volume of rotation of a region given by the height of a function
$r(x)$, about the $\displaystyle x$-axis:
\[
V
=\int_{a}^{b}dV(x)
=\int_{a}^{b}A(x)\ dx
=\int_{a}^{b}\pi r(x)^2\ dx
\]
If you're doing the rotation of a region other than one which "bottoms out" on
the $x$-axis, then you will be removing one volume from another -- which
is how you know that it should be
\[
V = \int_{a}^{b}\pi (R(x)^2 - r(x)^2)\ dx
\]
(rather than $(R(x) - r(x))^2$, which seems to be a fairly common
mistake). Here $R(x)$ represents the function on "top", while $r(x)$ represents
that on the "bottom" -- larger radius squared minus smaller radius squared.
See Matt's beautiful figure from Lab 3 below. The volume might be calculated as a large volume with a cylinder removed from its center.
- Physical area between two graphs of $\displaystyle f$ and $\displaystyle g$, from
$\displaystyle a$ to $\displaystyle b$:
\[
A
=\int_{a}^{b}dA(x)
=\int_{a}^{b}h(x)\ dx
=\int_{a}^{b}|f(x)-g(x)|\ dx
\]
The absolute value lets you be "lazy", since it doesn't matter which is on top
or which is on the bottom; but if you're doing it by hand, then you'll have to
find intersection points (if there are any) on the interval $(a,b)$, and
determine which is which.
Here $h(x)$ represents the height of a tiny rectangle at $x$, of width $dx$. Don't forget your "$dx$"s, as that always irritates the grader -- and you know that you should always keep your grader happy!
- The tangent line to $\displaystyle f(x)$ at the point $\displaystyle x=x_0$ is the graph of the function \[ tangent(x) = f'(x_0)(x-x_0)+f(x_0) \]
- The tangent line is an example of a linear approximation about the point
$x=x_0$: it's perfect at $\displaystyle x_0$, but usually gets worse the
farther you move away from $\displaystyle x_0$.
It's always good to ask yourself "Is my approximator still doing a good job?", and we answer that by comparing how the function and its approximator compare at points a given distance away from $x=x_0$.
Think of an approximator as a cheap way of getting a pretty good answer. Here's an analogy: in clinical trials the AstraZeneca vaccine was 70 per cent effective in protecting against symptomatic Covid-19. Pfizer's preliminary results suggest the shots are 95 per cent effective. Back in November, Pfizer treatment was going for about \$40; Astra for \$8.
- Critical numbers are those values of $\displaystyle x$ for which the first
derivative is zero or DNE (does not exist); they may be maxes, mins, or neither
(which we can determine using the first derivative test -- i.e., changes in the
signs of the slopes of tangent lines - or using the second derivative test --
i.e., concavity).
-
Inflection points are places where the concavity changes, and are found at
those values of $\displaystyle x$ for which the second derivative is zero or
DNE.
- Implicit differentiation allowed us to find the derivatives of most of our
inverse functions, using the inverse identity property.
Imagine that we know that $\displaystyle (e^x)'=e^x$, but don't know the derivative of $\displaystyle \ln(x)$, the inverse of $\displaystyle e^x$. Let's hope that we also remember the chain rule (and all those other rules from calc I!).
Since these two functions are equal (the identity rule for inverses), \[ e^{\ln(x)} = x \] their derivatives must be equal as well: \[ \left(e^{\ln(x)}\right)' = e^{\ln(x)} \left(\ln(x)\right)' = 1 \] Therefore \[ (\ln(x))' = \frac{1}{e^{\ln(x)}} = \frac{1}{x} \] Amazing!
- Volume of rotation of a region given by the height of a function
$r(x)$, about the $\displaystyle x$-axis:
\[
V
=\int_{a}^{b}dV(x)
=\int_{a}^{b}A(x)\ dx
=\int_{a}^{b}\pi r(x)^2\ dx
\]
If you're doing the rotation of a region other than one which "bottoms out" on
the $x$-axis, then you will be removing one volume from another -- which
is how you know that it should be
\[
V = \int_{a}^{b}\pi (R(x)^2 - r(x)^2)\ dx
\]
(rather than $(R(x) - r(x))^2$, which seems to be a fairly common
mistake). Here $R(x)$ represents the function on "top", while $r(x)$ represents
that on the "bottom" -- larger radius squared minus smaller radius squared.
p[x_]:=Log[3/(1 + x^2)]
xleft = -Sqrt[2]
xright = Sqrt[2]
z[x_]:=1
RevolutionPlot3D[{{p[x] + 1}, {z[x]}}, {x, xleft, xright}, RevolutionAxis ->
{1, 0, 0}]
Punch that in, and you'll see a beautiful volume of rotation about the line
$y=-1$:
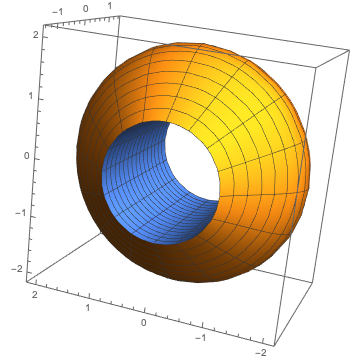
Looks like Matt actually shifted the function up one unit, then reflected it about the $x$-axis, and then removed a cylinder of radius 1 about the $x$-axis. This produces the identical figure, and its computed volume will be the same as the original object.