- I hope that your first exam went well this past weekend. I've not
looked at the exams, or the scores just yet. Should I?:)
If there are any particular issues we need to address, to make things better, please let me know.
I'll hope to have the exams graded in the next couple of days.
- Your Lab 3 is due tonight.
- Here we are, starting Week 4. Remember we didn't have a weekly assignment week 3, because of the exam; Hence, this week we encounter
weekly Assignment #3: due Monday, 2/8
(here it is as a .nb)
-
Today we review some basic integration rules, in preparation for some
new rules this week: integration by parts, and trig
substitutions. But for today we review a few of the rules from Calc
I.
- I want to remind you that there are section
summaries for the sections which we have studied to date, which
contain important formulas and highlights from each of the sections we
cover. If you haven't looked at those yet, you might take a peek.
(The ones featured in today's materials are actually from Calc I chapters of Stewart.)
- Here are our materials for today:
- Here are our materials for today:
- I just wanted to take another moment to actually invite you to
enjoy Matt's work on Lab 3. If you want to produce a beautiful
Mathematica version of that volume of rotation, then thank Matt Longwell, who provides this code:
p[x_]:=Log[3/(1 + x^2)] xleft = -Sqrt[2] xright = Sqrt[2] z[x_]:=1 RevolutionPlot3D[{{p[x] + 1}, {z[x]}}, {x, xleft, xright}, RevolutionAxis -> {1, 0, 0}]Punch that in, and you'll see a beautiful volume of rotation about the line $y=-1$: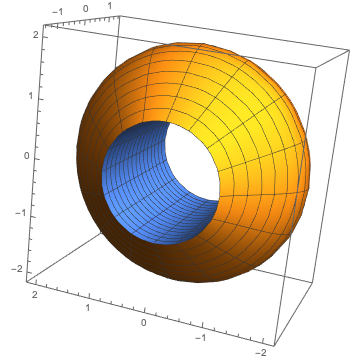
Looks like Matt actually shifted the function up one unit, then reflected it about the $x$-axis, and then removed a cylinder of radius 1 about the $x$-axis. This produces the identical figure, and its computed volume will be the same as the original object.