Day 13 in MAT229

• The parts were equally weighted, so compute your percentage by adding your scores, and multiplying by 100/80.

• As I described in an email, there were some issues with the IMath grading. I think that I've gotten them all squared away, but if you're wondering we can take a look at your exam.

  1. Here's an interesting mathematical issue: when is \[ \frac{1}{x+8}=\left(\frac{1}{\sqrt{x+8}}\right)^2 \]
  2. Another problem was my fault: I had the wrong answer built into the problem: it was about where this identity is correct: \[ x = \tan^{-1}(\tan(x)) \] and the correct answer (which most of you got) is $(\frac{-\pi}{2},\frac{\pi}{2})$.

• On the Canvas part, problems included
  1. Failure to show work, when it was requested. Show all your work -- it doesn't pay at all to hide any.
  2. I didn't count off for the following (but I will going forward):
     1. Failure to include parentheses in integrals, e.g. \[ \int \frac{x}{2}-x^2 dx \]
     2. Failure to include the infinitesimal (usually $dx$) in integrals, e.g. \[ \int \left( \frac{x}{2}-x^2 \right) \]
     Now some of you might think that those are nit-picky (I might have, when I was your age), but hopefully by the end of this section on integration (especially numerical techniques) you'll understand why they're so important. But here's the answer right up front: \[ \int \left( \frac{x}{2}-x^2 \right) dx \] The integrand $\left( \frac{x}{2}-x^2 \right) dx$ represents a product. What if I wrote the following quiz:
     1. $6*$ (correct answer: 6x)
     2. $2+ 3*6$ (correct answer: 30)
     Would you object? Well I'm objecting! And those are the things that you're writing when you leave off your parentheses, or $dx$.

     If you do these things, you're also messing up units. Check out the units in this volume integral: \[ V =\int_{a}^{b}dV(x) =\int_{a}^{b}A(x)\ dx =\int_{a}^{b}\pi r(x)^2\ dx \]

(here it is as a .nb)

So today we'll start by talking about indeterminate limits, L'Hopital's rule, and about some issues with integration (as we prepare to handle integrals that we couldn't handle before).

Note: problem 5c: revolve around the x-axis

	p[x_]:=Log[3/(1 + x^2)]
	xleft = -Sqrt[2]
	xright = Sqrt[2]
	z[x_]:=1
	RevolutionPlot3D[{{p[x] + 1}, {z[x]}}, {x, xleft, xright},  RevolutionAxis ->
	{1, 0, 0}]
	

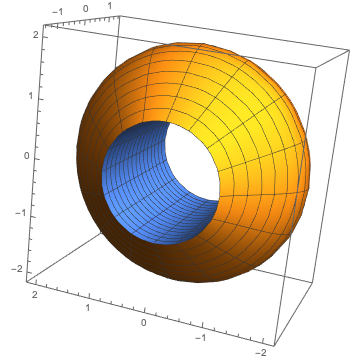
Looks like Matt actually shifted the function up one unit, then reflected it about the $x$-axis, and then removed a cylinder of radius 1 about the $x$-axis. This produces the identical figure, and its computed volume will be the same as the original object.