Day 01, Play-By-Play

Here's a link to a video, as I run through the thoughts below:

The class began with the usual rigamarole: syllabus, schedule, etc.
I did emphasize that this is a course usually populated by people who aren't that fond of math; and that this is not a traditional math course -- as evidenced by the presence of our friendly tetrahedron.
In this course, we will be studying beautiful and unusual mathematics. Yes, there will be some grubby bits; but there's a lot of beautiful mathematics, and we want to shine a spotlight on that.
We looked over a couple of logos. These are the kinds of things that you're going to be producing for yourselves. I think it's fair to think of it as something like a tattoo, only without the ink or the pain or the cost....
Those in-class will be presenting their logos with a two-three minute presentation at the end of the term; those on-line will be writing a paper, and putting theirs on Canvas.
The schedule is fairly well set: it will be the same for both sections; but assignments will differ by section; and the assignments listed are those for the in-class section.
Finally, when all the usual course-stuff was finished, we turned to the question of the day:

What do global warming and Covid have in common?
Okay, they're both really big problems -- that's true. And they're scary -- that's true. But can the Tetrahedron connect these ideas?
Before we got to that, I'd asked students to think of what they might do with a tetrahedron -- to what uses could they be put?
1. One student felt compelled to spin them!
2. One student felt compelled to wear one as a hat!
I had a few ideas up my sleeve, of course, and so I dragged those out.
1. Symmetry -- it didn't matter which "face" of the tetrahedron the student stuck her head through, because they're all the same!
  Each vertex (that's some of the "graph vocabulary" you're going to need to know) is the same as every other vertex (those are the balls on the corners of the tetrahedron).
  Each arc (or edge -- more terminology!) is the same as every other arc (or edge).
  So you can rotate a tetrahedron and you don't know it's been rotated -- because it comes back "into place".
2. Structural stability -- tetrahedra (that's the plural) are strong! In fact they're the backbones of some molecules....
3. We talked about how you could use a tetrahedron to compose music, assigning a note in a chord to each vertex (say).
4. We talked about how one could create a dance with dancers located at each vertex, connecting to each other by their own arms and legs. [And I reminded the students that one can always do an interpretive dance in lieu of a logo, if one wants...:)]
5. But, in particular, we talked about tetrahedron's role in global warming: it's the backbone of methane:
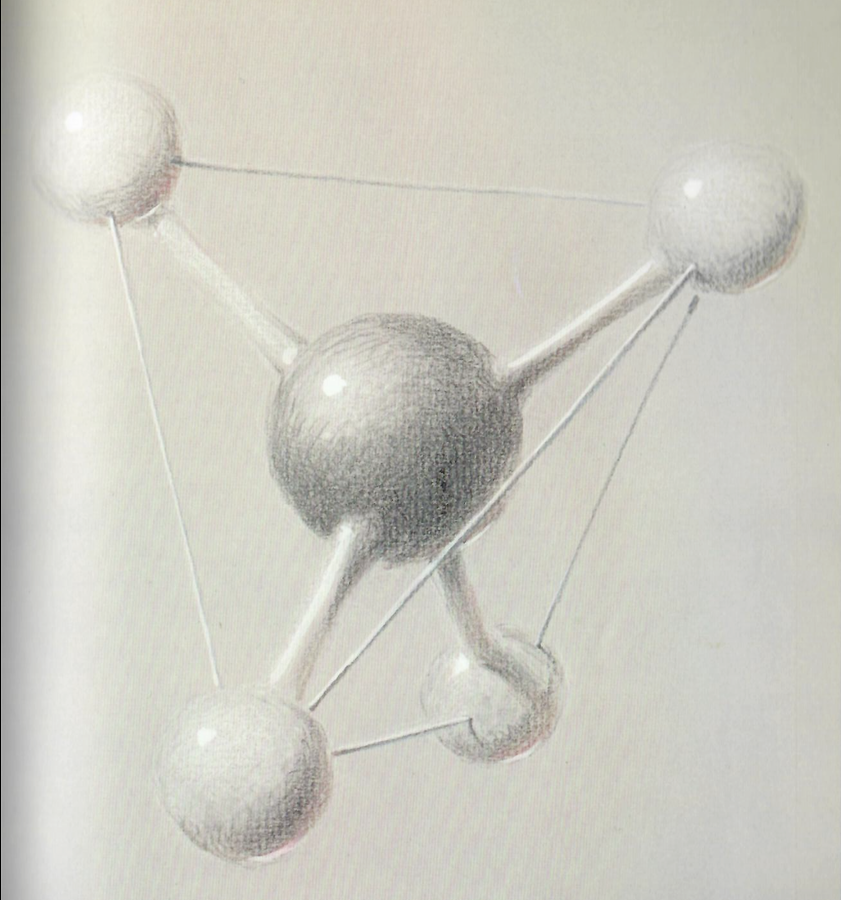
  Methane is a constituent of "natural gas": it's the stink of rotting landfills, or thawing permafrost. Those are some stinky tetrahedra!
6. So these molecules of methane are floating around up in space, reflecting Earth's heat back to the surface. Infrared radiation (that's how the Earth sweats) can't escape, and it's all because of these pesky tetrahedra -- well, the tetrahedra and others (such as CO₂).
7. Now what does the tetrahedron have to do with Covid-19? As I told folks in this session, the link isn't so tight there -- but we can use the tetrahedron as a model for social interactions, where the vertices (plural of "vertex") represent people, and the arcs represent connections -- physical contacts -- between the people.
  If no one is infected, then all is well; but if one of the people gets infected -- turns green, then the others are all at risk -- because they're connected to the green on. So those are the I of the SIR model; the S are the susceptible, and then there's the R: recovered, or removed. They don't contribute to disease transmission. Put them all together and we have an SIR model for a disease.
  The tetrahedron is serving as a model of the social structure for a disease -- an infectious disease, like Covid -- and we can use it to conduct a few thought experiments. For example,
  1. What happens if we double the number of infected people? That roughly doubles the number of contacts the susceptibles will have with ill people, and thus we expect to double the number of susceptible people who become ill.
  2. What happens if we double the number of susceptible people? (and here we got into a discussion of what it means to double; I meant that we double them in a room, so we're effectively doubling their density -- and so more get bumped into by the infectious, and so the number being infected will also double).
  3. I mentioned that this is the characteristic of a linear relationship. A linear relationship is one characterized by a line, and is one of the simplest kinds of relationship. But the way to recognize a linear relationship is this: if you double one of the variables, you double the other. So, for example,
    1. if you double the amount of gasoline in your car, you double the distance you can go.
    2. If you double the hours you work, and are paid by the hour, you double your gross pay.
    Those are linear relationships. Is it true that, if you double the quantity of ice cream you eat, you double your pleasure? This one breaks down at very large quantities of ice cream...:) So this relationship is not linear.
  More about this in our next class! (That's part of the details of the model for the disease.)
8. The key point, at this stage is that something like a tetrahedron can be very useful! And we'll learn more about them, and their mathematical natures, and their brothers and sisters (because tetrahedra are part of a family of such objects).
  And that this (probably) isn't the kind of math you've encountered in your lives up until now.
One final note: I said that we're going to be studying Covid modeling, in particular, because we want to understand why masking, and quarantining, and social distancing, etc. are important. So in our next class session, we'll try to indicate how those factors play a role in a simulation (numerical model) for Covid.

And I'll hope to have figured out how to use Zoom a little better, so that the "Zoom eye" isn't staring at a pointless whiteboard for most of the class...:(

Website maintained by Andy Long. Comments appreciated.