Day 8, MAT115

• This session will be captured on Zoom, if I remember to turn it on, and record it. Please help me to remember.

  Our a page of the zooms and the play-by-plays.

• Roll

• You have a new assignment (basically just a new IMath homework, due in a week).

• Your first IMath homework is due today (I pushed it back because of the snow day); I pushed it back a little further, because there seems to be a problem with #10.

• Sadly, water issues in our building forced the class to go "on-line", as many facets of numbers were examined, and dissected using Strogatz's "rock groups":
  • prime,
  • composite,
  • even and odd,
  • square, and
  • triangular numbers

• Here's a little more about the relationship between triangular numbers and the edges in complete graphs. Count the edges in the complete graphs, and what do you notice?

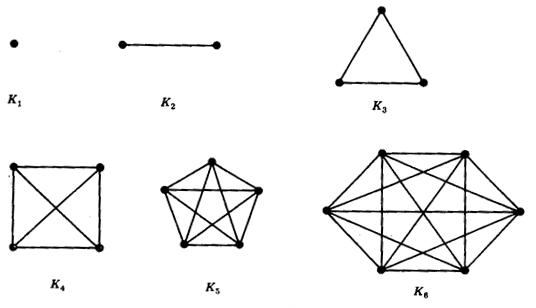
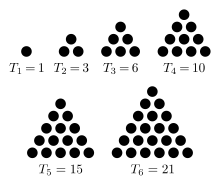
• The most important thing mentioned last time is the "Prime Factorization theorem¹":

  ---

  Every natural number (other than 1) is either prime, or can be expressed as a product of primes in exactly one way (in a unique way).

  ---

Again, the issue with 1 is that it ruins the uniqueness of the factorization if we make it prime. So we heartlessly cast it out!:)

• We're going to start today harkening back to the primes, by looking at how they are identified. Historically, the "Sieve of Eratosthenes" is the tool that was used (and that we'll use today).

  You might guess that Eratosthenes is a Greek mathematician, and you'd be right (actually born in Libya): but he was quite the scientist, too, and gave one of the first careful measurements of the Earth's diameter (even back around 200 BCE folks knew that the Earth was a ball...).

  Before we get to that, however, a bit of a review: I didn't get a chance to say enough about

  1. the power of primes (that they protect your bank account!); and

  2. twin primes, which were the not-quite-so-lonely primes -- are there infinitely many twin primes? (Mathematicians think so, but aren't sure yet!).

  3. "triplet primes" (3-5-7), of which there is only one set (and mathematicians are sure of that!).

  4. We used trees to try to understand primes:
     • Think of primes as isolated vertices (very lonely looking!) A prime number is its own "prime factorization".
     • We use trees to "expose" the unique "prime factorization" of composite numbers.
     We built some trees for a few numbers, and talked about how we can associate a unique tree with a unique counting number (this is the key idea between one-to-oneness -- a perfect dance, with everyone matched up with just one partner).

     So 6 has a unique factorization (2*3 -- ordered from smallest to largest), and a unique binary tree (created by factoring the number -- in this case, 6 -- by primes, from smallest to largest). The root of the tree is the number itself, and the leaves of the tree give the prime factorization:

     

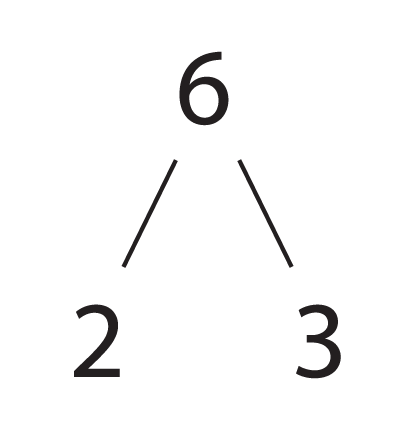
     In the end, there's this notion: there is a one-to-one correspondence between counting numbers and their prime factorizations (with primes as their own partners), and their labelled trees (and the tree seems to summarize -- or contain -- the other two!):

     6

     $\iff$

     2*3

     $\iff$

     But the tree also contains an algorithm for finding the prime factorization, based on checking to see if smaller primes are factors of the given natural number. In a moment, we'll try another one; but first let's see what this sieve of Eratosthenes is all about....

• Let's use the Sieve of Eratosthenes to generate all primes less than 100. While you do it, look for
  • The only two adjacent primes,
  • The triplet primes,
  • The twin primes,
  • "Spirals", and
  • The unprimiest looking primes!:)

• 
  "... each element in the first set corresponds to exactly one element in the second set and vice versa."

  These butterlies and flowers illustrate "fiveness": each set can be put into one-to-one correspondence with the sequence "1,2,3,4,5". And that's what counting is!:) Five is the number of flowers above; and the number of butterlies. That these are the same numbers is shown by the one-to-one correspondence, and our favorite set of five things is the set of symbols 1,2,3,4,5.

  Definition of

  Five. noun (plural fives).

  1. Merriam-Webster: A number that is one more than four.
     (Oh Lord! Work your way down, and this is what you get: one adjective: having the value of 1 (!). Ironically, "two" is an adjective as well....).

  2. Five is a number, representing any quantity of items that can be put into one-to-one correspondence with the sequence of symbols 1,2,3,4,5 (e.g. "Five is not the loneliest number; but it's the loneliest number since the number four.").

     Five can also be an adjective, describing five of an item (e.g. "There are five fish.").

  We have names for all the "counting numbers"; and as we count we frequently point, creating those connections between the numbers and the flowers, or butterflies, or cream pies, or spark plugs....

• Our authors show various schemes for recording the count. We use abstract symbols like "5". Other civilizations might show the same thing, only using a body part (right thumb), or tally stick, or a piece of knotted string.
  • 

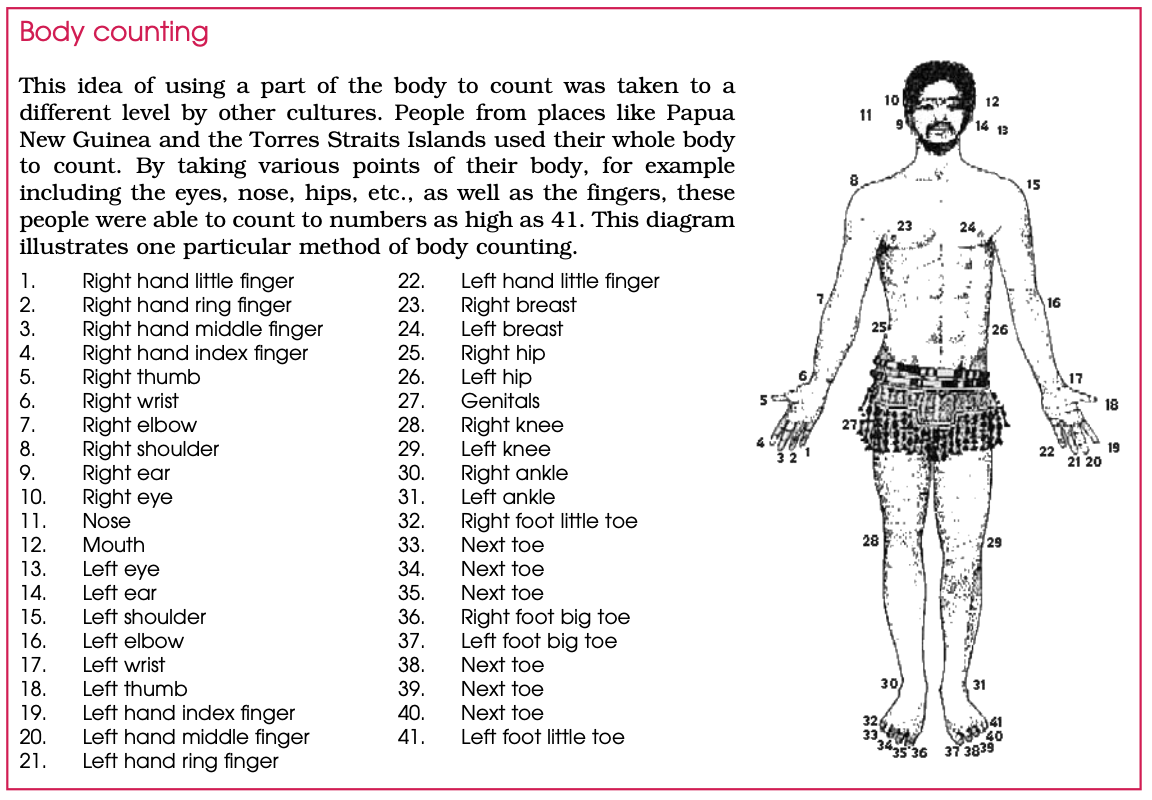
    I thought that this scheme was interesting, in that the scheme sort of goes "around the horn" (up and over the upper part of the body, from right to left); but then "back and forth" on its way down from the breasts to the toes.

    So it seems weird to me that one hand is 1-5, whereas the other is 18-22....

  • Knotted strings:

    Tally sticks:

• Now let's use a tree to find prime factors of 437.
  1. First a trick: you can start with 2, and, if you don't find any prime factors smaller than $\sqrt{437}$, you're done! It's prime.
  2. $\sqrt{437} \approx 20.9$; so if we find no factors less than this, 437 is prime.
  3. Here are the primes found in your sieve:
     2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97

  4. So let's do the tree....
  5. Special rules:
     1. Anything even is divisible by 2.
     2. Anything whose digits add to a number divisible by 3 is itself divisible by 3!
     3. Anything ending in 5 or 0 is divisible by 5.
     4. For the next primes, I use a "casting out" strategy:
        1. 7: think 420
        2. 11: think 440
        3. 13: think 390
        4. 17: think 340

• I'd hoped to get to "primitive counting", but I don't think that there's anyway that we will...:) Next time.

• The Sieve of Eratosthenes page at Wikipedia has an animated gif of the solution, which illustrates the procedure.