Day 7, MAT115

• This session will be Zoom only , because our building is closed due to a serious water issue.

  If NKU is closed Friday, due to weather, then we will not have class on Friday (even though it seems that we should -- just zoomed like we're doing today). That's the law, handed down by our Department Chair!:)

  Zooms and the play-by-plays

• You have an assignment for next time.

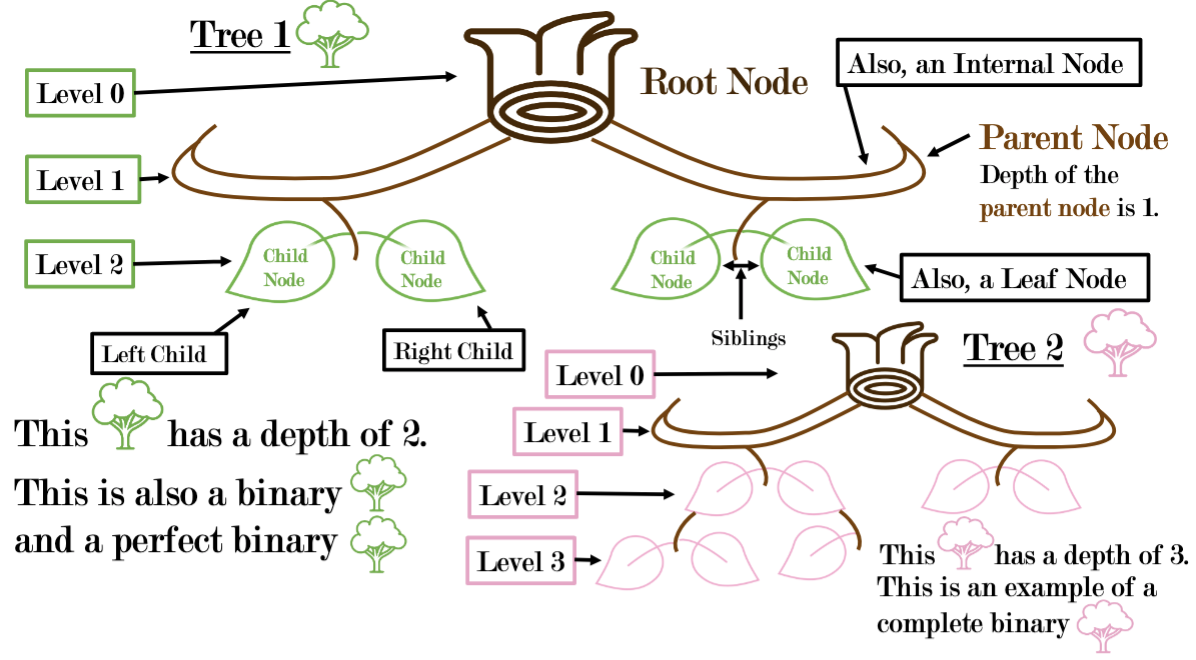
• You had an assignment (to illustrate our Tree Terminology page with your very own, beautiful illustrations!). My other section was expected to illustrate the graphs.

  I thought that we'd take a look at a couple of the "winning" entries.

  • Trees
  • Graphs

  In every thing we do in this class, I'm looking for you to express yourself. For that reason Amanda Murray is the grand prize winner:

  

• Your first IMath homework is due this Friday.

• We discussed the meaning of numbers, like "six". What is that thing?

  How do you know if something possesses "sixness"?

  It turns out that a key concept is that of a "one-to-one" correspondence, and that's what you're to read about, by next class. The reading is full of really interesting historical and anthropological information, much of which we'll touch on at some point in this course!. So it's worthwhile reading, for next time and into the future....

(The first -- of three -- great factorizations in mathematics that we'll look at.)

• Let's start to get at that question by considering Chapter 2 from our text: Rock Groups. To explore, it's good to use pennies (rather than rocks); or, better yet, M&Ms....:)

  We want to understand each of these notions:

  • prime,
  • composite,
  • square, and
  • triangular numbers
  but understand them as concrete things, as objects (e.g. pennies).

  So we're interested in arranging our pennies (i.e. rocks) in groups with certain properties.

  All numbers of pennies can be arranged into a line (this is Humphrey's "Furry Arms" method -- fish fish fish fish fish fish):

  

  But anything that "all numbers can do" is sort of uninteresting, in a way. It's so common!:)

• There is an interesting observation made by the author, about ways of putting coins into just two rows. It is about odd numbers and even numbers. What does Strogatz notice about the sum of
  • odd and odd
  • odd and even
  • even and even?
  He makes a nice rock group picture to help us to understand:
  

  Let's make a table to illustrate that:

  +	Odd	Even
  Odd
  Even

  Rock groups suggest formulas for representing even and odd numbers:

  Evens:	2*n
  Odds:	2*n+1

  It might be better to write them this way:

  Evens:	2*n+0
  Odds:	2*n+1

• Some numbers of pennies can be arranged into
  • rectangles (of more than one row):
    

    Recall that this is how Humphrey said the number of fish -- he blocked the fish into two groups of three fish --

    fish fish fish,
    fish fish fish

    (Notice that the penguins said "You got it!" -- they were able to count to six, evidently....)

    Numbers that can be represented as rectangles (with more than one row -- e.g. those six fish) are called "composite" numbers.

  • You'll know why squares are special if you make some with pennies: 1, 4, 9, 16, and so on.

    But Strogatz makes them in an interesting way, illustrating a theorem¹ in mathematics:

    

    One can conclude from this figure that a square number is the sum of a succession of consecutive odd numbers. Very odd, indeed!:)

    In this figure we see that \[ 5^2 = 1 + 3 + 5 + 7 + 9 \] You can SEE that it's true! You're convinced that it's true! (I hope....)

  • triangles lead to "triangular numbers".
    

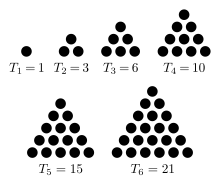
    But Strogatz builds these triangular numbers in such a way that you can again see a theorem:

    

    Triangular numbers are created by adding up consecutive integers: in the case of this figure, \[ 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55 = \frac{10*11}{2} \] Strogatz shows this in an unusual way: by doubling his work!

    

• Now, onto primes:

  If a counting number greater than one can be expressed as a rectangle with more than one row, then it is composite; otherwise, it is prime (for example the number 7).

  You can't express 7 as a rectangle, except as a single row of seven coins:

  

  Another way of saying that a number is composite is to say that it can be broken up into groups (each with more than one member) that can each be put into one-to-one correspondence with each other (that is, each element in one group has a partner in another -- and just one partner. Perfect for a dance....).

  You can try with 7:

  

  

  But you'll never succeed. (Rats.)

  So 25 is an example, a square. It can be broken into five groups of five, as we see in the figure above. Each of those groups of five matches up perfectly with the number of fingers on a hand, in a one-to-one correspondence; and perfectly with each other.

  Notice that we said greater than one in the definition above. The number 1 is special, and considered neither prime nor composite.

  We've already heard this important rule (theorem), which you probably learned at some point in your mathematical education, which is called the "Prime Factorization theorem":

  ---

  Every natural number (other than 1) is either prime, or can be expressed as a product of primes in exactly one way (in a unique way).

  ---

  If we allowed 1 to be prime, it would screw up this theorem! For example, we could write \[ 4=2*2 \] but also \[ 4=2*2*1 \]

  It would screw up the uniqueness! There wouldn't be "exactly one way" to write 4 as a product of primes (if 1 were prime). So we cast it out!

• At this point, we turn to "The Loneliest Numbers":
  1. One is the loneliest number, but that
  2. Two can be as bad as one; it's the loneliest number since the number one.
  And yet: two is a prime sitting right next to another prime -- three. They are the only two primes that touch -- how touching! (Sorry.)

  2 is also the only even prime -- because every other even number can be made into a rectangle with two rows in one-to-one correspondence -- a perfect dance -- and so every other even number is composite.

  As mentioned last time, some numbers seem very gregarious; they play well with other numbers (e.g. 6, which seems particular friendly with these touching primes, 2 and 3).

• Last time I asked How can we understand "6" without understanding "5" as well? (and thus 4, 3, 2, 1?)

  And I suggested that we might use complete graphs to understand these counting numbers:

  

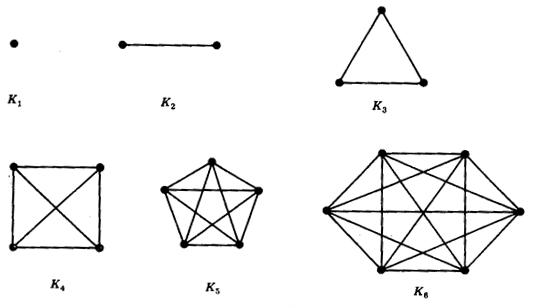
  If we think of counting numbers that way, we can see that "two" ($K_2$) contains two copies of "one" ($K_1$); "three" ($K_3$) contains three copies of "two"; etc.

  There are six copies of "one" within "six" ($K_6$). Can you see the $K_4$ can be thought of as a tetrahedron? Can you see the five tetrahedra within five ($K_5$)?

• However, primes may allow us to understand "six" without understanding all the numbers that come before: it will only be necessary to understand the prime numbers.

  Let's use trees to try to understand them.

  • We'll think of primes as isolated vertices (very lonely looking!) A prime number is its own "factorization".
  • We'll build trees to show the prime factors of composite numbers.
  We'll end on some examples, and get back to these next time. Let's build some trees for
  • 5
  • 6
  • 24
  • 56
  In the end, there's this notion: there is a one-to-one correspondence between counting numbers and their prime factorizations (with primes as their own partners).