Day 10, MAT115

This session will be captured on Zoom, if I remember to turn it on, and record it.

Our page of zooms and the play-by-plays.

This magic trick, carried out with the help of six simple cards, no doubt amazed and astonished you, and made you think "Hmmm... maybe there's money to be made here!"

I have 11 Togolese shirts. Suppose I put them into a strict rotation, each school day a different shirt (M-F, five days out of seven), and I repeat the cycle through the end of the semester.... Will you see each shirt before the end of the semester?

• Hint/Easier: What if I had 10 Togolese shirts?
• Hint/Easiest: What if I had 1 Togolese shirt?:)

It turns out that The Great Fraudini can read anyone's mind -- so long as they're thinking of a number between 1 and 63, and they're willing to play a little card game with him. So let's recall how this works.

• Rules of the game: you show your "victim" every card. If they see their number on it, they say "Yes"; otherwise they say "No". Then you tell them their number!
• Here's a handout for the cards.
• Each card has a unique power of two in the upper lefthand corner: add up the powers of two, and you've got their number. But how do we know that there aren't two numbers that appear on exactly the same two cards?

  That would completely mess things up, right? We get to that in a moment.

A method of "counting by partitions" that Patricia Baggett and Andrzej Ehrenfeucht proposed at the 2011 National Math Meetings. Here's how it works:

1. divide your sheep equally ("one for you, one for me") into two pens: either there is one sheep left over, or not.

   You make a note of whether there is a leftover sheep or not -- maybe you make a mark, like a "1" or a "0"; or maybe you tie different knots in a string (more on knots later in the course). This is all you have to do to communicate the number to the King! You don't need to know how to count, to our way of thinking.

2. Send all the sheep in pen two (and any "left over") out to pasture, and then
3. You divide the remaining sheep into pens one and two: i.e., just do it again! And again, and again, and.... until you get down to a pen with just one sheep in it.
4. Then we send our marks off to the King, perhaps on a tally stick.

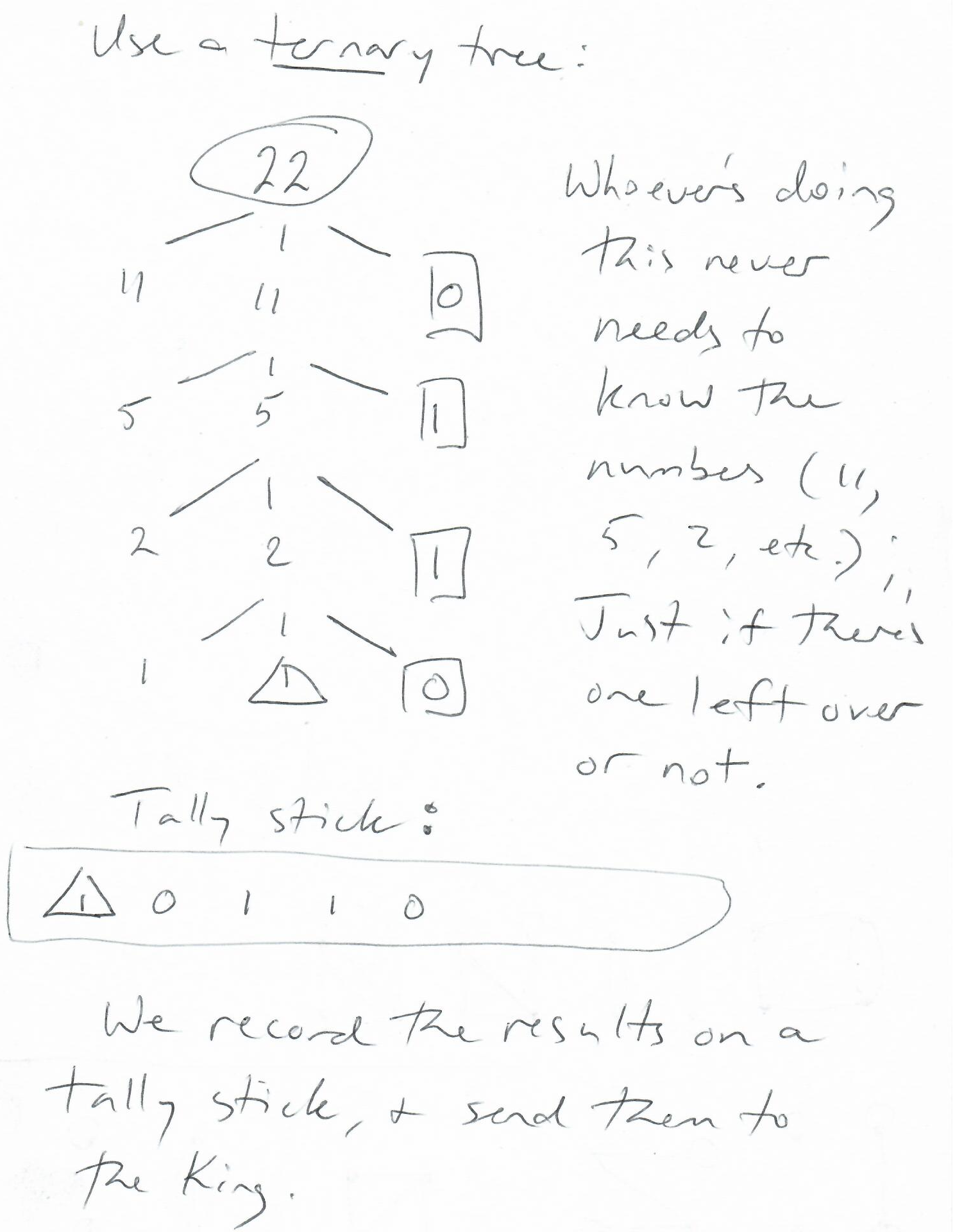
I say "Whoever's doing this..." -- I mean, "Whoever's doing this primitive counting...." This is presumably someone who doesn't know how to count -- at least not the way we do -- but they can tell if there's a sheep left over (and write "1") or not (and write "0").

Notice that we eventually have a single sheep in a pen, and that's when we're done. We have to write a "1" for the final sheep, to indicate that there's "one leftover".

Then the answer will be written as 1, 0, 1, 1, 0. That is, from the bottom up, left to right. This is important! We have to have a consistent scheme for writing.

So how do we write

• 27 sheep
• 390 sheep

• 1,0,1,1
• 1,1,0,1,1,0,0
• 1,0,0,1,0,1,1,0,1

(Notice that, while there can be either a 0 or 1 at the right end, there is always the "1" on the left -- meaning the last sheep standing!

Can you rebuild the tree using these "tally sticks"? If so, you can get a job in the King's counting house. Let's rebuild some....

But rather than count out fifty pennies, I'd make a stack of 10, then four more stacks of exactly the same height (one-to-one correspondence). Five stacks of 10 makes 50. This is a similar idea....

If you have a lot of pennies, you could divide them in half, count half, and then multiply by two. But if you have one left over, you'd have to add that one.

If the half is still too many to count, do it again (on half), and so on -- until you get to the point where you can count "the half" (like if it gets down to 1 coin, say!:).

The secret of Fraudini's trick is another secret of the counting numbers, 1, 2, 3, 4, ....: the binary factorization of a number.

This is the second great factorization of the counting numbers. So it turns out that the counting numbers and sums of distinct powers of two can be put into one-to-one correspondence (if we count single powers of two as "sums"...).

Here are the first few powers of 2:

\[ \begin{array}{l} 2^0 = 1 \cr 2^1 = 2 \cr 2^2 = 4 \cr 2^3 = 8 \cr 2^4 = 16 \cr 2^5 = 32 \cr 2^6 = 64 \cr 2^7 = 128 \cr 2^8 = 256 \end{array} \]

(Do you see why the Great Fraudini can only read numbers up to 63?)

So in base 10 we think of "17" as \[ 17 \textrm{ (one ten and seven ones) } = 1*10 + 7*1 = 1*10^1 + 7*10^0 \]

That last bit on the right shows 17 as a sum of "weighted" powers of 10 -- "weighted" because we have to say just how many ones we need (7 of them in this case). For binary numbers the "weights" are easy: 1 or 0.

17 appears only on the 1 card and on the 16 card. We figure out how to write a number as a sum of powers of 2, and then we write that number on each of those cards. And then it will be the only number exclusively on those cards -- and the sum will tell me the number!

\[ 17=1+8+8=2^0+2^3+2^3 \] So we could write \[ 17=1*2^4+0*2^3+0*2^2+0*2^1+1*2^0 \] or, better yet, $17_{10} = 10001_2$ -- 17 base 10 is equal to 10001 base 2.

I always tell people to write their salaries in base 2, because they look a lot bigger! More impressive.... All of a sudden you find yourself making six or seven figures!

• Let's start easy with 97 (a big prime!).
• Now let's use a tree to find the binary factors of 437.

1. the "1" card is all the odds -- every odd number will have to include a 1. You can think of that as a skip of one.

2. The "2" card starts 2,3, then skips two (because 4 picks up the slack!).

4. The "4" card starts 4,5,6,7, then skips four (because 8 picks up the slack).

8. The "8" card starts 8,9,10,11,12,13,14,15, then skips eight (because 16 picks up the slack).

16. The "16" card starts 16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31, then skips sixteen (because 32 picks up the slack).

32. The "32" card starts (and ends), with 32 numbers from 32 to 63 -- at which point 64 would have picked up the slack, had we wanted to use more than six cards.

Vi Hart has the most amazing ways of showing us interesting mathematics. She shows us that we can count to 31 on one hand. And, if you'll use the 10 fingers of two hands, you can get all the way up to $2^{10}-1=1023$...

Some people can only count to 10 with their fingers....