- the fact that we can probably figure out what 9 looks like. We can see the counting numbers, running down the diagonals after the diagonals of ones.
- the existence of a 0 -- in fact, that their "bamboo counting rods" writing has 10 looking exactly like our 10, only on its side!
- We figured out the error we'd identified in the triangle last time -- a 34, instead of a 35, was written by the creater of Yanghui's triangle. The scribe missed a stroke.
- We noticed that there is place value: there is a tens place, and a ones place. It's used to make numbers from 10 up. We can presume that there's a 100s place, too -- we just didn't have any numbers that big.
- We then used the back side of the sheet (the honeycomb pattern on
the reverse side) to make a more modern version, called Pascal's
triangle:
If you click on that image, it will take you to a page that will tell you perhaps more than you want to know about Pascal's triangle:). But we'll know about all that stuff, by the time the course is over....
Notice the asymmetry in their colors -- they could have run from left to right, just as well. The number patterns are the same, right and left.
The first diagonal set of numbers they left out in the image above is called the tetrahedral numbers:
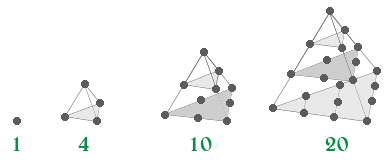
Also the boardwork shows some of those connections. We connect Pascal's triangle up to binary trees, which we can think of as containing the results of tossing coins (Heads or Tails). Pascal's triangle shows, for each depth of the tree, how many different tosses lead to each type of result -- all heads, all heads but one, ..., all tails but one, all tails.
| n | # of possible edges | # of Facebook configurations |
| 1 | 0 | 1 |
| 2 | 1 | 2 |
| 3 | 3 | 4 |
| 4 | 6 | 11 |
Furthermore, we saw that each configuration has a "dual" configuration, given by the rule that "If there's a connection (edge), break it; if there's no connection, make it!"
