-
- This session will be captured on Zoom, if I remember to turn it on, and record it.
- Our page of zooms and the play-by-plays.
- Roll
- You have a new assignment.
- Your third IMath homework assignment is
due Monday.
- You have a homework assignment due Friday (to submit on Canvas).
We reviewed the binary factorization, and then explored "Yanghui's triangle" (and you should look yours over carefully):
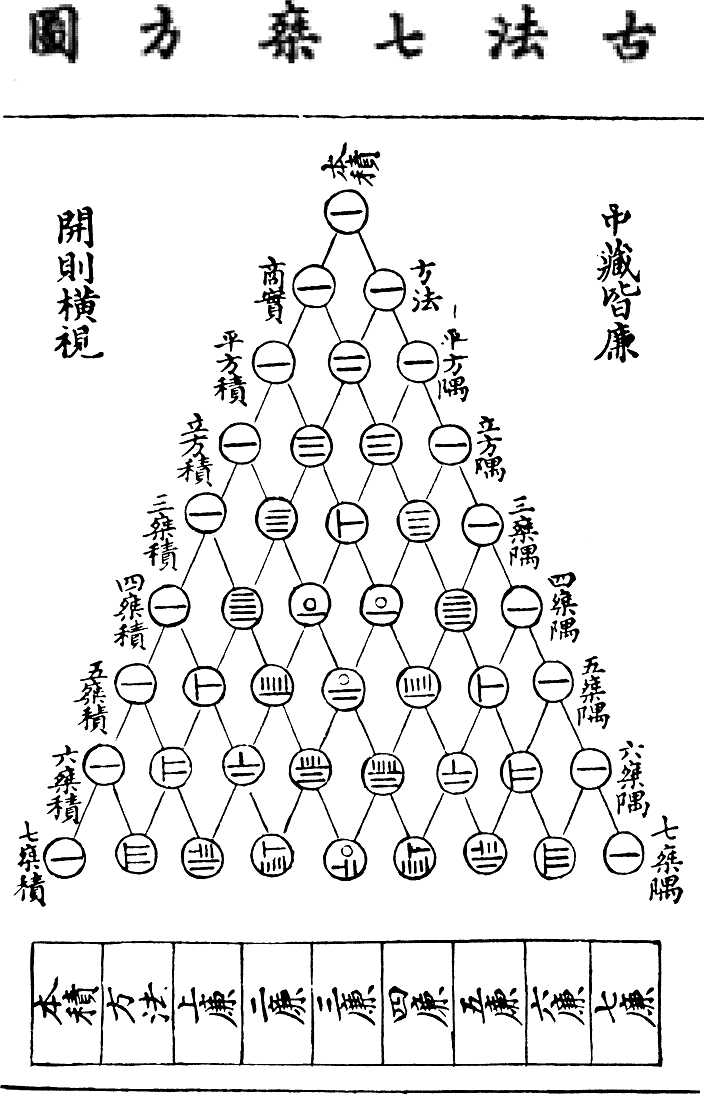
- Students quickly suggested several things (which we call "conjectures"):
- Horizontal lines represent "1"
- Vertical lines represent "5"
- That if you sum up rows, you get a power of two!
- That the rule is "add the two above, right and left, to get the next number.
We attempted to verify these rules, and managed to find that they are consistent; we couldn't contradict the rules -- although Becca noticed that there's a problem in the next to last row.
Upon closer examination, we discovered that there is an error in the table! Whoever wrote this, in 1200 AD or so, must have made a little mistake, and lost a stroke. See if you can find it.
We'll talk more about symmetry as we get further into the course, but here's one place where it really shows up. Because we expect the table to be a mirror reflection of itself, left and right, we can spot errors -- where the symmetry breaks down.
But there are still some "open questions", which we haven't figured out. I asked you to try to answer some questions (mathematicians look for patterns):- What do you notice? What catches your attention?
- Can you find any number patterns?
- Can you understand the writing system for numbers?
- What is this thing? What is its purpose?
There were still some open questions about the bamboo counting rods way of writing numbers. Let's nail those down first. How does this writing work?
- Let's create a more modern version of this triangle on the
back of your sheet (I hope that you brought your sheet back). It's
called "Pascal's Triangle", after Blaise Pascal.
- Let me make a connection to trees, because Bradley noticed that it
seems to resemble a tree. In particular, I want to relate it to binary
trees.
One can also think of this as a connection to "Plinko" (if you've ever heard of that); and to something called a Galton Board. (I'll show off my "Hexstat Probability Generator" -- which shows you that Pascal's triangle is also very closely tied to probability calculations, too.)
Imagine flipping coins for each ball: heads, go left; tails, go right. Let's draw the decision tree.
Pascal's triangle simply doesn't care if you go right then left, or left then right: you end up in the same plinko spot. So Pascal says "2 ways to do that". "1 way to get HH", "1 way to get TT", but two ways to get a head and a tail (HT and TH). Pascal's triangle just does the accounting: \[ 1 \hspace{1in} 2 \hspace{1in} 1 \] The next row is the ways of getting three heads, two heads, one head, and no heads: \[ 1 \hspace{1in} 3 \hspace{1in} 3 \hspace{1in} 1 \]
And, by counting the leaves of the binary tree, we see that it's always a power of 2! So the sum of the rows of Pascal's triangle has to be a power of 2.... Now we understand Emilee's "power of 2" rule;
but also the rule about where adding the "two above" to get the value in the next row. That's the plinko rule!:) Or the Hexstat rule. Where do balls come from at any point in the triangle? From the two spots right above.
- vertices (or points, which we will think of as people), and
- edges (which are also called arcs, connecting two points -- which we will think of as friendships).
Now, if we don't care about "who's who", then we can see all the different types of Facebooks we can have:
- Let's look at some simple cases: 2 or 3 individuals
- All simple graphs with four vertices.
- All simple graphs with five vertices.
- Now, if we add names to the "vertices", then we have more
Facebooks. If each person is friends with everyone else, then
the graphs we can get will look like this:
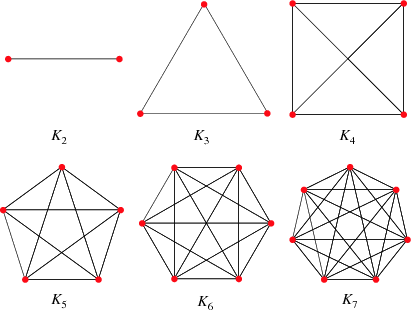
Now how many different Facebook configurations are there for, say
- 2 individuals?
- 3 individuals?
- 4 individuals?
- The upshot is that a row of Pascal's triangle tells us
how many different ways we can choose $p$ objects from amongst
$n$. This is why it was so useful to Pascal in his gambling
exercises....
For example, there is only one way to choose all; and only one way to choose none! Those are the easy cases. It should be obvious that there are $n$ ways to choose 1 from among $n$; or to leave one out of $n$ (note the symmetry).
- In the case of Facebook, we're looking at setting up friendships, which are relationships between n people. So we look to the row containing the number of friendships possible between $n$ people, which is the triangular number $\frac{n(n-1)}{2}$. That row tells us how many different Facebooks we can have with any given number of friendships.