Day 13, MAT115

• This session will be captured on Zoom, if I remember to turn it on, and record it.

  Our page of zooms and the play-by-plays.

• Roll

• You have a new reading assignment.

• Your third IMath homework assignment is due Monday.

• Next Friday is our first exam. Start reviewing!

• You have a homework assignment due today (to submit on Canvas -- as a single pdf is best).

We created a more modern version of Yanghui's triangle, called "Pascal's Triangle" -- named after Blaise Pascal, who studied it extensively.

• We connected Pascal's triangle to trees; binary trees, in particular, formed by tossing coins (say); and we linked it to playing "Plinko". The paths in Plinko lead to gates, and the number of ways to reach any particular gate is a number in Pascal's triangle.

  Pascal's triangle simply doesn't care if you go right then left, or left then right: you end up in the same Plinko spot. So Pascal says "2 ways to do that". "1 way to get HH", "1 way to get TT", but two ways to get a head and a tail (HT and TH). Pascal's triangle does the accounting: \[ 1 \hspace{1in} 2 \hspace{1in} 1 \] The next row is the ways of getting three heads, two heads, one head, and no heads: \[ 1 \hspace{1in} 3 \hspace{1in} 3 \hspace{1in} 1 \]

  And, by counting the leaves of the binary tree, we see that it's always a power of 2! So the sum of the rows of Pascal's triangle has to be a power of 2.... Now we understand Emilee's "power of 2" rule;

  but also her rule about adding the "two above" to get the value in the next row. That's the plinko rule!:) Or the Hexstat rule. Where do balls come from at any point in the triangle? From the two spots right above.

• Now it turns out that Pascal's triangle is very useful in the study of graphs. We talked about what I called "Facebook graphs":
  1. vertices (or points, which we will think of as people), and
  2. edges (which are also called arcs, connecting two points -- which we will think of as friendships).
  It turns out that Pascal's triangle gives all the ways of having a "Facebook" for any number of indivduals.

  Now, if we don't care about "who's who", then we can see all the different types, or "configurations", of Facebooks we can have.

  • We had a look at some simple cases: 1, 2, or 3 individuals. And we saw that, in those cases, there were 1, 2, and 4 possible different configurations. If you're a mathematician, you're probably going to guess "8" for the case of four people; but it turns out to be 11!

    (That's weird, and the sort of thing that gets mathematicians up in the morning, and keeps them up at night.)

  • All simple graphs with four vertices. Here it is, showing the duality a little better.
  • All simple graphs with five vertices.

    I produced this picture so that the "duals" of each graph appear reflected about the middle column.

    Note that the graphs in the middle column have to have duals in the middle column (and some of the graphs are self dual -- can you see which ones?).

  A simple graph is a way of connecting people -- either two are connected or not. The question is, how many different ways are there of having Facebook for $n$ distinctly different individuals?

• If each person is friends with everyone else, then the graphs we can get will look like these: complete graphs. We need to imagine that there's a unique, different person at each vertex. (And notice that I've added $K_1$: the loneliest Facebook, when it was just Mark Zuckerberg, all alone.)
  

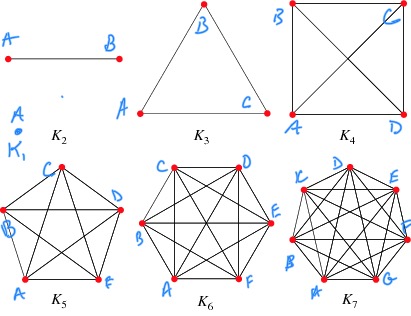
  Now how many different Facebook configurations are there for, say

  • 2 individuals?
  • 3 individuals?
  • 4 individuals?
  How do we use Pascal's triangle to find the answer for a given number of people? We actually use it in two ways:
  1. to identify the correct row to examine (the story of Gauss -- Prince of Mathematicians); and then,
  2. to read from that row the number of different ways of having a given number of Facebook friendships.

• Here's the upshot of what the numbers in Pascal's triangle do for us: if we look at the $n^{th}$ row, then the $p^{th}$ entry in that row tells us how many different ways we can choose $p$ objects from amongst $n$.

  Both $n$ and $p$ start from 0: that is, there is a zeroth row, and a zeroth entry (thinking left to right, say). So the "1" at the top of the triangle is the zeroth entry in the zeroth row, and it tell us how many ways there are to choose 0 elements from a set with 0 elements: 1!:)

  After that, things make a little more sense: so in the next row, you discover how many ways to take objects from a set with 1 element: you can take none in 1 way, and all in 1 way.

  This way of thinking about the numbers is why the triangle was so useful to Pascal: for his gambling habit!

  Think about cards, for example. It's all about "how many ways":

  • How many ways can I get a flush?
  • How many ways can I a straight?
  • How many ways can I four of a kind?
  Think about dice:
  • How many ways can I roll doubles?
  • How many ways can I roll primes?
  • How many ways can I get snake eyes?

  For $n$ objects,

  1. there is only one way to choose all
  2. there is only one way to choose none!
  3. (Those are the easy cases, and they explain those diagonals of 1s along the left and right edges of the triangle.)

     Hopefully it's also clear that there are $n$ ways to choose 1 from among $n$ things;

  4. just as there are $n$ ways to leave one out of $n$ (note the symmetry -- the duality).

• In the case of Facebooks, we're looking at setting up friendships (edges), which represent relationships between pairs of people. This is the triangular number $\frac{n(n-1)}{2}$.

  So we look to the row containing the number of friendships possible between $n$ people.

• Let's look at a concrete example: 4 people give rise to 6 possible friendships: \[ \frac{4*(4-1)}{2} = \frac{4*3}{2} = 6 \] So we look to that row (let's call it the "six row" -- the one starting 1, 6, ....) to tell us how many different Facebooks we can have with 6 people. Let's do a little drawing....

  We won't draw them all, because there are $2^6=64$ different Facebooks! (11 different configurations, but 64 distinct version of those 11 configurations.)

  Here's a start...

• While we only get Facebooks for $n$ individuals from those rows which can be expressed as triangular numbers, the other rows are useful, too. For example, if you want to know how many ways there are to invite five friends to dinner (or not), you check out the "five row" of Pascal's triangle:
  0. friends: 1 way (to invite no one -- boring!)
  1. friends: 5 ways (to invite just one special friend)
  2. friends: 10 ways (to invite your two favorite)
  3. friends: 10 ways (to leave out your two least favorite)
  4. friends: 5 ways (to leave one out...:(
  5. friends: 1 way (to leave no one out! Yes! Do that!)

• Yanghui's triangle (and hexagons for making one of your own)
• Pascal's version