Day 14, MAT115

• This session will be captured on Zoom, if I remember to turn it on, and record it.

  Our page of zooms and the play-by-plays.

• Roll

• Your third IMath homework assignment is due today.

• You have no new assignments up to the exam.

• This Friday is our first exam. Start reviewing! We'll be reviewing together on Wednesday. Come with questions.

• I have graded the Canvas assignment. Questions? (Here's a key, thanks to Camryn -- with one small change -- she forgot to add the 11 to the prime factorization of 2310. It's in the tree, but she forgot it in the list.)

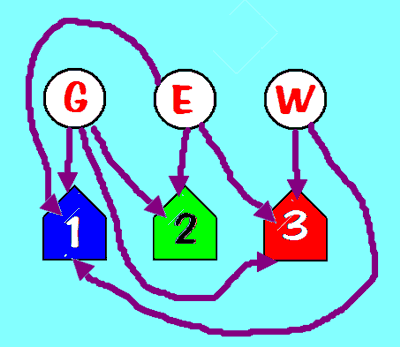
• We reviewed Facebook graph configurations, ignoring names.
  • All simple graphs with four vertices, showing the duality with colors.
  • All simple graphs with five vertices.

    I produced this picture so that the "duals" of each graph appear reflected about the middle column.

    Note that the graphs in the middle column have to have duals in the middle column (and some of the graphs are self dual -- can you see which ones?).

  • Becca had a great way of characterizing dual graphs: they complete each other -- together they make the complete graph, with no redundancy. Each is fully responsible for some of the connections (the edges). Together they cover all of the edges.

• Then we added names to the "vertices", and were able to read the different Facebooks possible. It was a two-stage process:
  • Start with the number of distinct individuals, $n$.
  • Look up the triangular number $e=\frac{n(n-1)}{2}$. This is the number of edges in the complete graph with $n$ vertices.
    

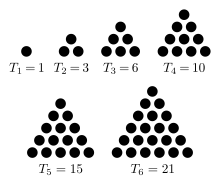
    (Notice that this even works for $K_1$ -- use the $0^{th}$ row!)

  • Now this is what Pascal's triangle does for us: if we look at the $e^{th}$ row, then the $p^{th}$ entry in that row tells us how many different ways we can choose $p$ objects from amongst the $e$ edges.

    And each distinctly different choice of edges (friendships) leads to a different Facebook!

• More generally: for $n$ objects,
  1. there is only one way to choose all
  2. there is only one way to choose none!
  3. (Those are the easy cases, and they explain those diagonals of 1s along the left and right edges of the triangle.)

     Hopefully it's also clear that there are $n$ ways to choose 1 from among $n$ things;

  4. just as there are $n$ ways to leave one out of $n$ (note the symmetry -- the duality).

• While we only get Facebooks for $n$ individuals from those rows ($e=\frac{n(n-1)}{2}$) which can be expressed as triangular numbers, the other rows are useful, too. For example, if you want to know how many ways there are to invite five friends to dinner (or not), you check out the "five row" of Pascal's triangle:
  0. friends: 1 way (to invite no one -- boring!)
  1. friends: 5 ways (to invite just one special friend)
  2. friends: 10 ways (to invite your two favorite)
  3. friends: 10 ways (to leave out your two least favorite)
  4. friends: 5 ways (to leave one out...:(
  5. friends: 1 way (to leave no one out! Yes! Do that!)
• As another example, to find out how many poker hands you can make from a standard 52 card hand, you go to the row of Pascal's triangle that starts "1 52 ..." and you pick off the sixth entry in ("How many ways to choose five cards from 52?"): that number, if you were to write Pascal's triangle out to that row(!), would be \[ 2598960 \textrm{ hands} \] By the way, that works out to 52*51*50*49*48 divided by 5*4*3*2*1. And from that, you might be able to guess how every number in Pascal's triangle is computed! (Remember that the triangle is symmetric).

We'll look at a few new graph definitions, and play a couple of "games" with graphs

• Really important: graphs don't change by bending edges, but breaking them or detaching edges from their vertices (and hence creating new vertices) gives new graphs.

• Recall that a graph is simple if it doesn't have any loops (edges connected from a vertix to itself), or multiple edges with the same two vertices.

• The Bridges of Konigsberg problem: "is it possible to set off and walk around Konigsberg crossing each bridge exactly one?"
  

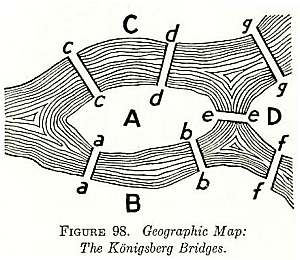
  Notice that this graph is not simple (like our complete graphs).

  • Solved by Euler (1735), this was the beginning of graph theory.

    How do we know? It comes down to degrees of vertices. Recall:

    The degree of a vertex is the number of edges coming into it.

  • Let's see if we can figure out Euler's solution.

    One thing Euler noticed was the hand-shaking theorem: in any graph, the number of vertices with odd degree must be even.

    Can you explain why?¹

  • An alternative solution to Euler's problem (thanks to spiked math)

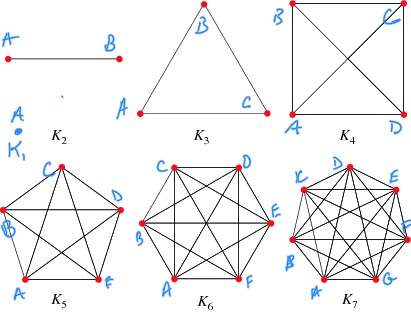
  • Which of the complete graphs above can be traversed without backtracking? What about the pentagram ($K_5$):

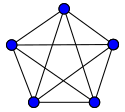
    (You've probably been drawing graphs for a long time....)

  • If you can traverse a graph's edges without backtracking, you've created an Euler path. Euler paths only exist in graphs for which there are either exactly 0 or 2 odd-degreed vertices. If a path exists, and if there are 2 odd-degreed nodes, then the path will begin at one and end at the other.

    As you can see, the Konigsberg bridge graph has 4 nodes of odd degree.

• Planar graphs

  • New definition: Planar graphs are graphs that can be drawn such that no two edges intersect. Which of our complete graphs are planar?

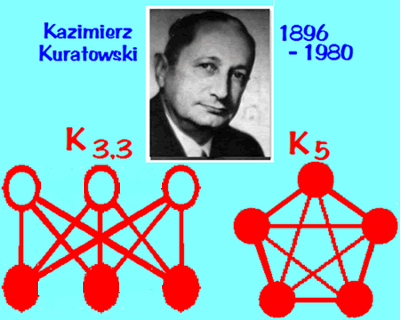
  • Exercise: Let's see if we can show that $K_5$ is not planar:
    • Why not? What happens?
    • We can show that the complete graph with four vertices is planar (remember, we can bend edges!).
    • The three utilities and three houses graph is not planar:

    • Kuratowski's theorem: Any non-planar graph has a copy of one of these two graphs in it somewhere, as a subgraph:
      

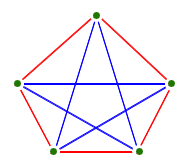
• Yanghui's triangle (and hexagons for making one of your own)
• Pascal's version