-
- This session will be captured on Zoom, if I remember to turn it on, and record it.
- Our page of zooms and the play-by-plays.
- Roll
- You have no new assignments up to the exam, which is this Friday.
- Today we'll be reviewing.
- Here's a key to the Day 11 homework, thanks to Camryn -- with one small change -- she forgot to add the 11 to the prime factorization of 2310. It's in the tree, but she forgot it in the list.
- We looked at a few new graph definitions, and played a couple of
"games" with graphs -- introducing the idea of "Euler paths" and planar
graphs.
- Really important: graphs don't change by bending edges, but
breaking them or detaching edges from their vertices (and hence
creating new vertices) gives new graphs.
- Recall that a graph is simple if it doesn't have any loops (edges connected from a vertix to itself), or multiple edges with the same two vertices. The graphs we look at in the next two problems include graphs which are not simple (although the complete graphs are simple).
- The Bridges
of Konigsberg problem: "is it possible to set off and walk around Konigsberg crossing each bridge exactly one?"

As you can see, the Konigsberg bridge graph has 4 vertices of odd degree.
There is only an Euler path if a graph has either 0 or 2 vertices of odd degree. If there are two odds, then you will start the path at one, and end it at another; if there are no odd vertices, then you will start and end at the same vertex (and create what is called an Euler cycle).
- Really important: graphs don't change by bending edges, but
breaking them or detaching edges from their vertices (and hence
creating new vertices) gives new graphs.
- Planar graphs
-
New definition: Planar graphs are graphs that can be drawn such that no two edges intersect. Which of our complete graphs are planar?
- Exercise: $K_4$ is planar: it can be drawn without false intersections.
- Exercise: $K_5$ is not planar:
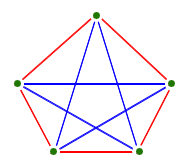
- The three utilities and three houses graph is not planar:
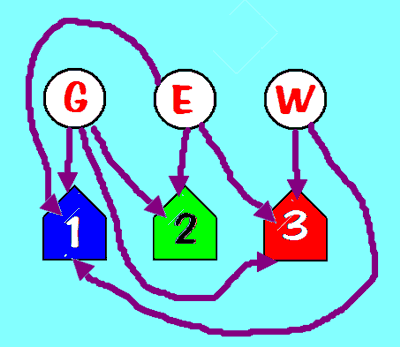
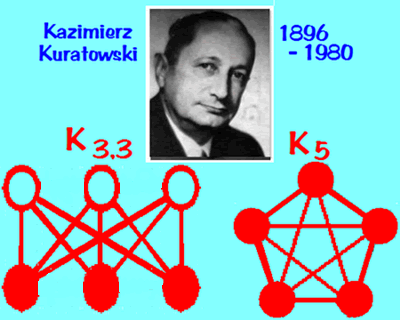
- Kuratowski's theorem: Any non-planar graph has a copy of
one of these two graphs in it somewhere, as a subgraph:
-
- Let's start with your questions.
- Then I'll give you a quick summary of what we've done so far, and
what to expect:
- First of all, you'll be expected to do problems
similar to the problems that you've submitted
(to Canvas, and to IMath): you shouldn't be
surprised by what you see.
- You will be expected to have done the readings,
and you'll see questions related to the
readings.
These will not be things buried in the text, but that were out in the open. If you've read them, you should know them. Nonetheless, it wouldn't hurt to review them.
- You might take a run through the daily
agendas, to remind yourself of what we've done
these past few weeks.
- In terms of topics, as I went through those agendas here's
what I turned up:
- The tetrahedron -- model for methane, and a graph ($K_4$) helping us envision how infection in covid occurs. We've seen this old friend often, and it will come back again!
- Covid modeling: SIR models
- S-I-R: the role of each
- linear relationships
- $R_o$
- how do masking, quarantining and vaccinating people impact the model?
- Insightmaker results: endemic versus eradicated
- Graph Terminology
- Tree Terminology
- Strogatz's weighted graphs (stability):
the enemy of my enemy is my friend, and the friend of my enemy is my enemy - true vaccination rate: Two-toss sampling
- Natural frequencies: breast cancer
- Testing: false positives, false negatives; sensitivity and specificity
- What is six? How do we understand numbers? Sesame Street!
- Rock groups:
- Even, odd
- Squares
- Triangular numbers
- Primes
- Composite
- Complete graphs $K_i$ (such as the tetrahedron)
- Sieve of Eratosthenes
- Prime factorization, using binary trees
- Twin primes -- not quite as lonely
- One-to-one correspondence
- Body counting, tallies, knots, cairns
- The Great Fraudini, and powers of 2
- Primitive counting, using ternary trees
- The Binary factorization, using binary trees
- Binary hand dancing!
- Yanghui (and Pascal's) triangle
- Counting "how many ways" with Pascal
- Pascal and the number of Facebooks
- Containing counting numbers, triangular numbers, and even tetrahedral numbers; binary numbers as sums of rows.
- Dual graphs, complete graphs, and Facebook configurations
- Glimmers of symmetry
- First of all, you'll be expected to do problems
similar to the problems that you've submitted
(to Canvas, and to IMath): you shouldn't be
surprised by what you see.
- There won't be problems about the Bridges of Konigsberg, or planar graphs.
- Yanghui's triangle (and hexagons for making one of your own)
- Pascal's version