- This session will be captured on Zoom, if
I remember to turn it on, and record it. Please help me to remember.
I've created a page of the zooms and the play-by-plays.
- Roll (if I don't have a note card for you, let me know.)
- You have a new assignment (to illustrate our Tree Terminology page
with your very own, beautiful illustrations!). That will be due Sunday
night; that way I can bring some to class on Monday and show them off
(he said, hopefully!). You'll submit those on Canvas as pdfs.
On Friday I'll issue your first IMath homework, which will cover the material we've done so far.
- On a very sad, and timely note, the climate scientist Lisa
Goddard has died, age 55, and the cause was breast cancer....

Ironically, I learned it just moments after doing the play-by-play for this chapter. Argh....
- We were talking about your reading (Chapter 3: the Enemy of my
Enemy), visualizing diplomatic relations (positive and negative)
between countries in Europe with graphs, in the build-up to WWI.
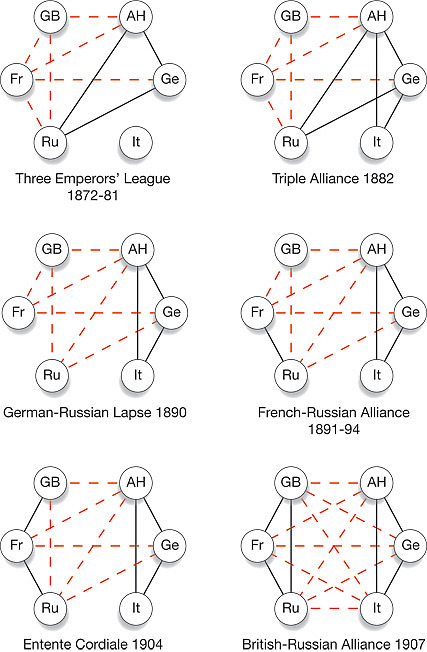
"He [Putin -- i.e. Russia] well recognizes that Europe's main power base is France, Germany and Britain... If these three countries are united, the rest of Europe follows. If you can sow divisions among these three, then there's no leadership, there's no coordination and there's no unity."
In the article, they discuss the warming relations between Germany and Russia, etc. So they're talking about those edges on that graph between all the countries -- positive, negative, neutral?
- We then went on to consider a method for sampling a population to
discover vaccination rates, which allow for individuals to "hide" (if
there's embarrassment, say) -- we want to provide cover, so that
individuals feel comfortable reporting "honestly". Except that we allow
people to lie!:)
So it's based on randomness and lying, and we use trees to illustrate the situation (Tree Terminology).
- After conducting our experiment, tossing a coin twice, and
flipping our answer if it comes up heads, we made an estimate of the
true rate of vaccination for the class. But....
I messed up the final calculation! In my hurry to "beat the clock", I made an error which resulted in an estimate of 40% for the vaccination rate of NKU students. (Can you find my error?)
In actuality, the estimate should have been 70%. Big difference! Here is the proper calculation:
The measured rate of vaccination was $r_v$, which got a contribution of $\frac{3}{4}r$ from the vaccinated, and $\frac{1}{4}(1-r)$ from the unvaccinated: \[ r_v=\frac{3}{4}r + \frac{1}{4}(1-r) \] Now we solve that for $r$: \[ r_v=\frac{1}{2}r + \frac{1}{4} \] or \[ r_v - \frac{1}{4} =\frac{1}{2}r \] Solving for $r$, we get our final formula:
\[ r=2\left(r_v - \frac{1}{4}\right) \]
- In the example problem we considered, we presumed an
$r_v=\frac{65}{100}$, and an $r=\frac{80}{100}$. Let's see if we get
that value of $r$. We plug into the formula, and get
\[
r =2\left(\frac{65}{100} - \frac{1}{4}\right)
=2\left(\frac{65}{100} - \frac{25}{100}\right)
=2\frac{40}{100}
=\frac{80}{100}
\]
Perfect!
- Now we did our experiment in class, with our 15 valiant students, and found an $r_v=\frac{9}{15}$; we plug into the formula, and get \[ r =2\left(\frac{9}{15} - \frac{1}{4}\right) =2\left(\frac{36}{60} - \frac{15}{60}\right) =2\frac{21}{60} =\frac{42}{60} = 0.7 \] So 70%! Much better vaccination rate, more in line with what I've been led to believe about our student population.
- In the example problem we considered, we presumed an
$r_v=\frac{65}{100}$, and an $r=\frac{80}{100}$. Let's see if we get
that value of $r$. We plug into the formula, and get
\[
r =2\left(\frac{65}{100} - \frac{1}{4}\right)
=2\left(\frac{65}{100} - \frac{25}{100}\right)
=2\frac{40}{100}
=\frac{80}{100}
\]
Perfect!
- Tricky math! Our author says as much; doctors struggle with this
stuff (and they've had plenty of calculus, and a stats class,
etc.). We're talking about probabilities (and randomness, again!), and
conditional probabilities to boot.
- Although there is a general method of solving these things, our
author suggests that it's better to make very specific examples to do
our calculations ("Break a difficult problem into easier ones."). So
that's what we'll do.
- Just as we did last time we're going to start by drawing some
pictures of the situations -- the trees. There are two problems
we're going to consider today. We start with the problem of the plant,
which we will treat with trees: perfect, binary trees.
- The story of the plant, and the three questions:
- What's the chance your plant will survive the week?
- If it's dead when you return, what's the chance that your friend forgot to water it?
- If your friend forgot to water it, what's the chance that it will be dead when you return?
There's one especially important thing that Strogatz introduces into the discussion: estimation. Sometimes its just a good estimate we're after -- not the answer to six decimals.
- Now, to the crucial question of the day: you've gotten
awful news, but you're aware that there are false
positives, and false negatives. You're hoping for the
former. "What are my chances, Doc?"
And Strogatz says, basically, don't bother asking. They don't know! (Scary thought....)
But we can figure it out! (Maybe we should go to medical school.) Here's the situation; the data:
- In this group (your "cohort"), 0.8% of women have breast cancer.
- If you have breast cancer, this test will catch it 90% of the time (10% false negatives!).
- If you don't have breast cancer, this test will tell you that you do 7% of the time (false positives).
Your physician here in the US tells you it's around 75%1, so you go home devastated. Turns out it's 9%. Let's see how to "see" that!
- The story of the plant, and the three questions: