Day 3, MAT115

• This session will be captured on Zoom, if I remember to turn it on, and record it. Please help me to remember.

  Here's today's zoom, and the Play-by-Play

  Here's the day02 play-by-play. I had to redo what we did in class, because I forgot to record it, but it might be good to see it again.

• Roll (if I don't have a note card for you, let me know.)

• You have a new assignment: Read Chapter 23: Chances Are in your text. This is a challenging read. As I say in your assignment page, "don't sweat the details! There's some challenging math in here. We're going to talk about it.... But try to get the big picture."

• Let's do a quick summary of what we discovered last time:
  • Graphs serve as models, and we'll see a lot of graphs throughout the course. (For that reason, I've created a Graph Terminology page for you.)

  • Simple mathematics leads to fairly realistic behavior (e.g. waves of disease).

    In particular we modelled "Linear stuff": if I double $x$, do I double $y$? If so, the relationship is linear.

    We concluded that new infections are linearly related to both the size of the infected population, and the size of the susceptible population.

  • While the virus has a certain "$R_o$" associated with it, meaning that an infected individual will infect a certain number $R_o$ of additional individuals, we can drive down that number with societal decisions -- e.g. masking, quarantining -- to make it effectively smaller, which may allow us to eradicate the disease.

    Vaccines, on the other hand, essentially set up a pathway directly from susceptible people to recovered people -- removing them as prospective targets of Covid, and cutting into new infections.

    What we know from SIR models is that Public health requires public-level solutions.

• What questions do you have?

• As I said, this gives us some exposure to the use of graphs to model interesting situations
  • The curious rules of multiplication of positive and negative numbers
  • European diplomatic relations in the run-up to World War I.

• Let's categorize the graphs of the European powers, using some of our Graph Terminology:
  

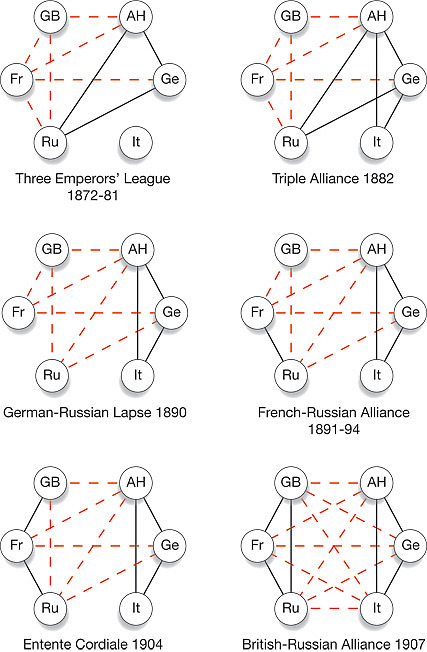
• Now, an example from my own life (and you try to think of one from your own!)

(and let's forget about boosters -- just the first round)

• You are probably aware that I'm not supposed to ask any of you that question directly. But, just as public health benefits from public-level solutions, I can pool your information and make a pretty good guess -- without knowing any individual's status!

  So your privacy is respected, but we also get a good idea of how well vaccinated you are as a group.

• This approach will rely on several things:
  1. Trees,
  2. Randomness, and
  3. Lying.
  Here's a picture of a random tree, lying down:
  

  :) Is is comforting to know that we're relying on that stuff? Maybe trees sound best, but these aren't the trees you're probably thinking of. Instead, they're a kind of graph (surprise!).

  Here's your Tree Terminology page. You should learn those definitions. I'll be using some of them today, and will give you some definitions as we go.

  When you do your reading for next time (Chapter 23: Chances Are), you might try to imagine how I'm going to use trees to help illustrate what the author describes (Strogatz could have used some trees to make things clearer!).

• So let's get to the trees, and randomness, and lying. (I'll be using the Whiteboard, and will save the work we do on it to a file which I'll post here. I'm not real pleased with how that pdf looks when I save it...)
  • We're going to start by drawing some pictures of the situation -- the trees.

    One experiment we'll pass on, because it doesn't allow enough lying; the second one will allow everyone to lie!:) We'll go with that...

  • Then we'll do an experiment, with random coin tosses

  • Finally we'll estimate the true rate of vaccination for the class.

    NB: important! I messed up the final calculation! I was in a hurry to "beat the clock", and made an error which resulted in an estimate of 40% for the vaccination rate of NKU students. (Can you find my error?)

    In actuality, the estimate should have been 70%. Big difference! Here is the proper calculation:

    The measured rate of vaccination was $r_v$, which got a contribution of $\frac{3}{4}r$ from the vaccinated, and $\frac{1}{4}(1-r)$ from the unvaccinated: \[ r_v=\frac{3}{4}r + \frac{1}{4}(1-r) \] Now we solve that for $r$: \[ r_v=\frac{1}{2}r + \frac{1}{4} \] or \[ r_v - \frac{1}{4} =\frac{1}{2}r \] Solving for $r$, we get our final formula:

    ---

    \[ r=2\left(r_v - \frac{1}{4}\right) \]

    ---

    1. In the example problem we considered, we had an $r_v=\frac{65}{100}$; we plug into the formula, and get \[ r =2\left(\frac{65}{100} - \frac{1}{4}\right) =2\left(\frac{65}{100} - \frac{25}{100}\right) =2\frac{40}{100} =\frac{80}{100} \] Perfect!

    2. Now we did our experiment in class, with our 15 valiant students, and found an $r_v=\frac{9}{15}$; we plug into the formula, and get \[ r =2\left(\frac{9}{15} - \frac{1}{4}\right) =2\left(\frac{36}{60} - \frac{15}{60}\right) =2\frac{21}{60} =\frac{42}{60} = 0.7 \] So 70%! Much better vaccination rate, more in line with what I've been led to believe about our student population.

• Last time:
  • Our Covid simulation from InsightMaker
  • Gotta catch those sneezes!
  • Wear a good mask
• Today:
  • Graph Terminology
  • Tree Terminology
  • One-toss sampling technique
  • Two-toss sampling