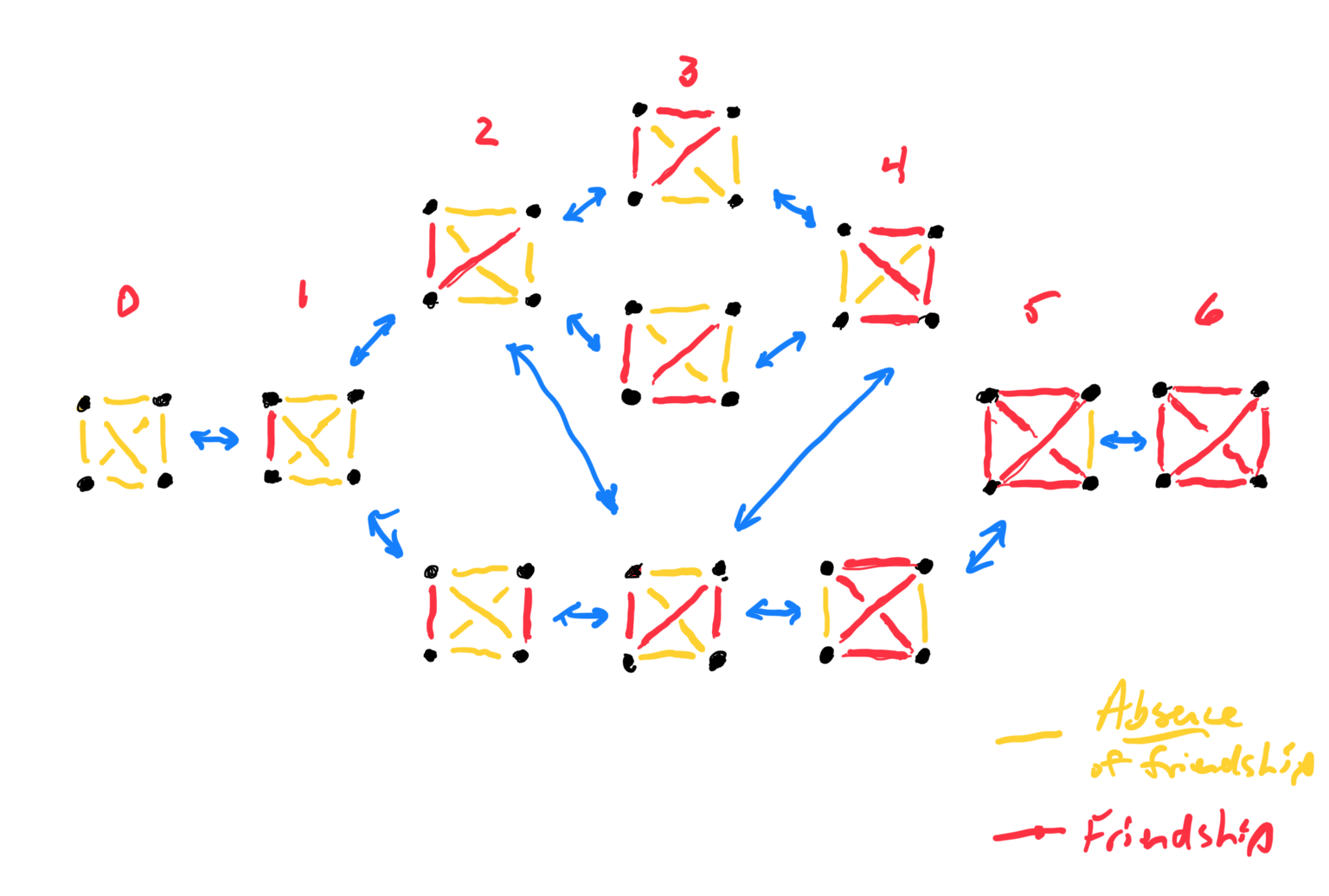
We talked again about duality between the configurations, and how to get from one to another. The key idea is if there is a connection (edge) in one graph, you break it; if there's no connection, you make it; and that produces the dual.
So the completely isolated graph is the dual of the complete graph, etc.
This is important for gambling -- lots of games. How many ways of rolling doubles in dice? How many ways of getting a heart flush in cards?.
In this case, we're looking for the number of Facebooks if we have named individuals (it's always a power of 2!). But that's no surprise, since all the different configurations are given in a row of Pascal's triangle.
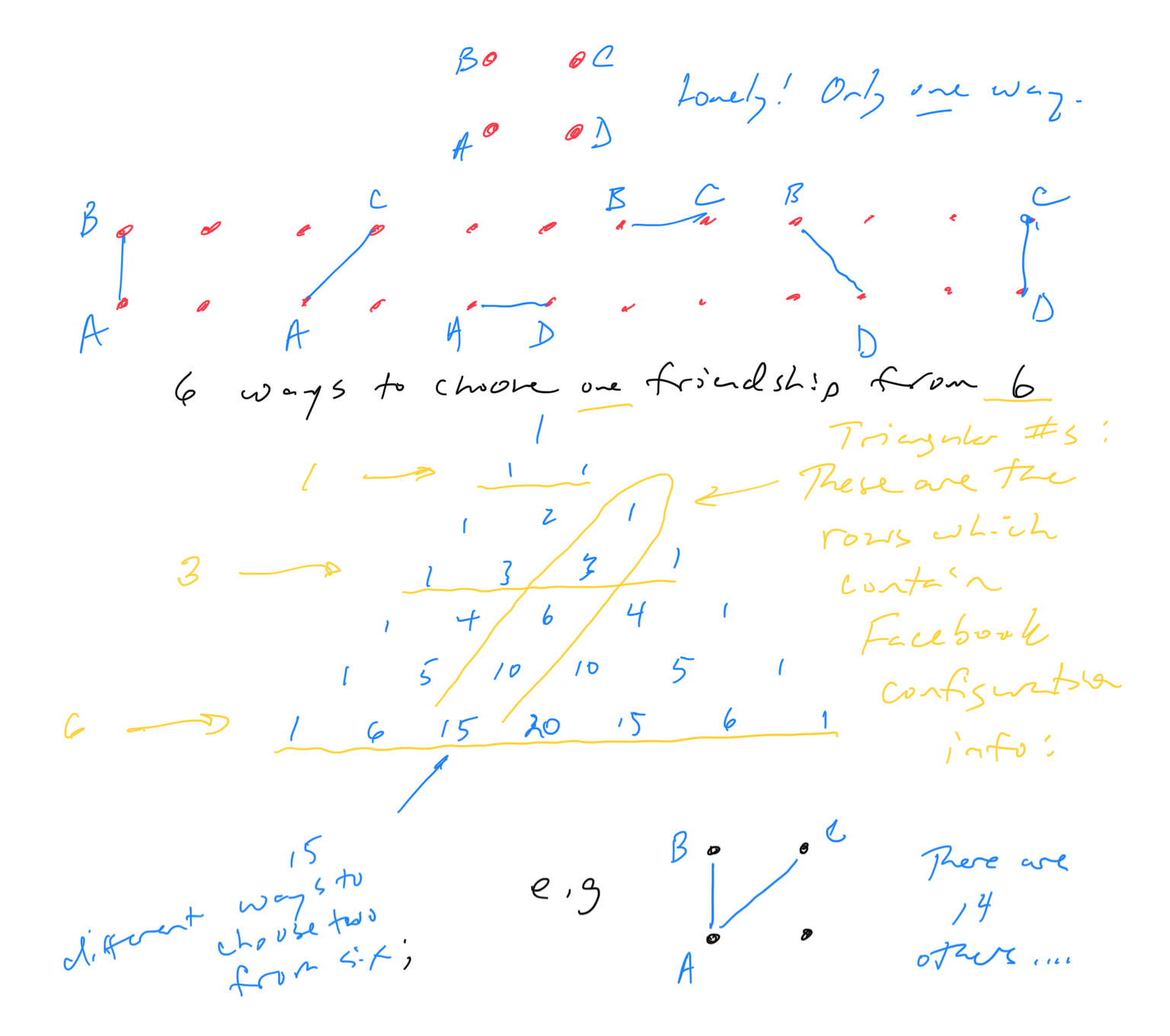
For example, to find out how many poker hands you can make from a standard 52 card hand, you go to the row of Pascal's triangle that starts "1 52 ..." and you pick off the sixth entry in ("How many ways to choose five cards from 52?"): that number, if you were to write Pascal's triangle out to that row(!), would be \[ 2598960 \textrm{ hands} \] By the way, that works out to 52*51*50*49*48 divided by 5*4*3*2*1. And from that, you might be able to guess how every number in Pascal's triangle is computed! (Remember that the triangle is symmetric).