If you have questions about any of the things we've studied so far, you might send me an email; I'd include those in our review on Wednesday.
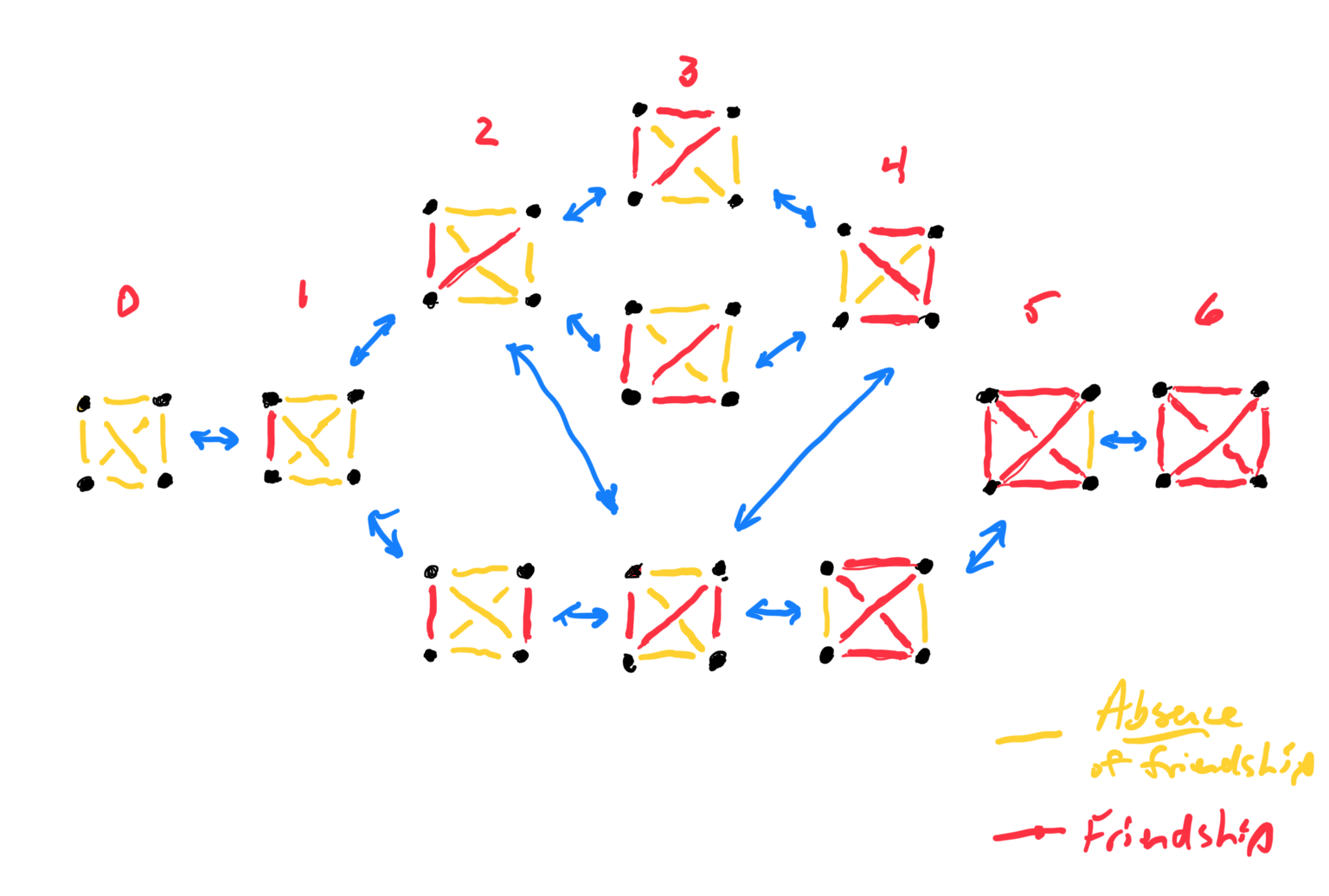
It's about deciding how many edges (friendships) to include, and then the different ways one might do that. For example, in a facebook of four people you can use the three friendships to make a chain (the middle bottom configuration), or you could create a super-social individual (the middle middle configuration),
So if you want to know how many ways there are of choosing 3 cookies from a plate of 7 cookies, it's 35. And the number of ways of choosing 4 cookies is also 35 -- because it's the same as choosing 3 cookies to leave on the plate, while you make off with the four cookies.
There are 21 ways to choose only 2 cookies (but why limit yourself? Take 3 or 4 cookies!).
Both $n$ and $p$ start from 0: that is, there is a zeroth row, and a zeroth entry (thinking left to right, say). So the "1" at the top of the triangle is the zeroth entry in the zeroth row, and it tell us how many ways there are to choose 0 elements from a set with 0 elements: 1!:)
- Euler paths -- paths around a graph where each edge is traversed exactly once; and
- Planar graphs: graphs which can be drawn without any edges making any false intersections.
- Euler paths:
If you did your reading, then I would encourage you to try to draw this graph (Euler's bridges of Konigsberg graph, at right below) without retracing any edges, or lifting your pencil:
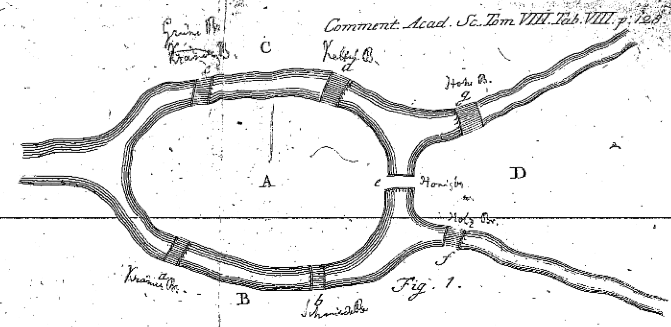
(If you didn't do your reading, I'd do your reading first!).
The question is, when can this be done; under what conditions on the graph? See the notes for day 14 for the solution.
- Planar graphs: graphs which can be drawn without any edges
making any "false" intersections.
Really important: graphs don't change by bending edges, but breaking them or detaching edges from their vertices (and hence creating new vertices) gives new graphs. So the question is, can you bend and twist some edges to get them out of the way, so that they don't appear to overlap each other?
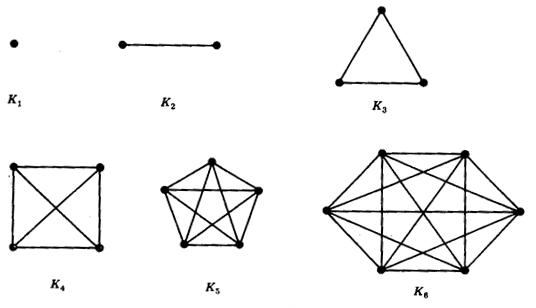
Try to draw the complete graphs $K_4$ through $K_6$ without false intersections: you can't do it for them all. At what point does it break down? Why?
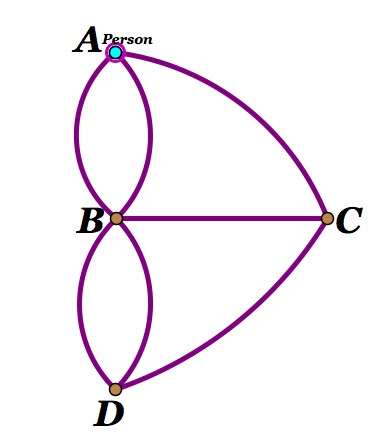
We then went on to discuss the three houses and three utilities graph: try to draw it without false intersections.
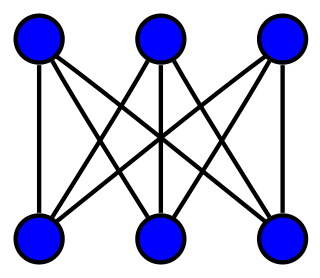
It turns out that there's a theorem (Kuratowski's theorem) about which graphs are planar graphs, and you can find it on our Day 14 page.