Day 21, MAT115

• This session will be captured on Zoom, if I remember to turn it on, and record it.

  Our page of zooms and the play-by-plays.

• You have an IMath assignment due this Friday, 3/18.

• Last week we must wear the masks in class; and then I think that I, at least, will be maskless. You will be welcome to mask or not in class, as of 3/21.

• Babylonian and Mayan review, including a couple of examples.

• Then, a start to Egyptian mathematics.

We began with Egyptian multiplication, which is based on the fact that the Egyptians didn't mind doubling things: that was easy for them; and that's the key to Egyptian multiplication.

Successive doublings means powers of two, so this reduces to the Fraudini trick! That's the good news.

• We began last time with a simple example: multiply 23*42.

  We double the larger of the two, generally, and use the binary factorization of the other to choose which rows to include in the final answer (indicated by the asterix):

  23=16+4+2+1

  1 42 * 2 84 * 4 168 * 8 336 16 672 * 32 Too big!

  672+168+84+42 = 966

  Now add up those rows marked with an asterix (*), and you'll get the answer (966 = 23*42).

  This works because of the distributive rule: \[ 23*42 = (16+4+2+1)*42 = 16*42+4*42+2*42+42 = 672+168+84+42 = 966 \]

• Let's show that we can do a multiplication in either order, by checking the product 42*23. (What is "too big" in this case?)

  1	23
  2
  4
  8
  16
  32
  64
  128	Too big!

• Let's try a longer multiplication. Consider, for example, 321*112:

  1	321
  2
  4
  8
  16
  32
  64
  128	Too big!

  Add up those rows marked with an asterix (*), and you'll get the answer (35952).

• Let's move on to division.
  • Multiplication's not too bad. How about Egyptian division?
    • I've assigned this reading to do while working on your homework: it includes some material which you've already seen elsewhere, but also includes information on the Egyptians, and, well -- it just seemed really interesting!

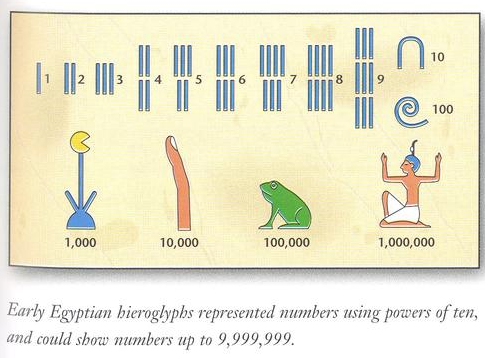
    • This figure from the reading shows how ancient Egyptians wrote their numbers. (Notice the blocking; and that, like us, they're base-10 people!)
      

    • Then, at the end of the reading, how they wrote fractions:
      

  • As we approach division, we'll start with the easy ones -- where one number is actually evenly divisible by another.

    We can think of division as just using the multiplication table "backwards". So if we write the quotient (which is what we're looking for) as \[ \frac{dividend}{divisor}= quotient \] We can think of this as a product instead: \[ divisor*quotient = dividend \] For the product we take one of the parts of the product (the divisor, say), and double it in the center column. Making up the other part of the product (the quotient) with powers of two, we then find the product (the dividend) by adding up the corresponding numbers from the center.

    In the division problem we know the dividend, so we reverse the process: we find numbers in the center that sum to the dividend, and then add up the corresponding powers of two on the left to give the quotient, which is what we're after.

    Example: Let's try this one from last time (rather than 23*42(=966), suppose you want $\frac{966}{23}$(=42)).

    1	23
    2
    4
    8
    16
    32
    64	Too big!

  • Let's look at the simplest example imaginable: divide 32 by 8. We can actually do it by Egyptian multiplication, since 8 divides into 32 evenly:

    1	8
    2	16
    4	32	*

    So the answer is 4 (how do we get 4?)

  • Similarly we could divide 40 by 8, using the same table (again easy, since 8 divides into 40 evenly):

    1	8	*
    2	16
    4	32	*

    So the answer is 5 (how do we get 5?)

  • Now: what happens when the division doesn't work out quite so nicely? We get "the f-word": fractions!

    • When the denominator doesn't divide the numerator evenly, fractions make it more interesting (my word -- you might use a different word!:).

      Let's look at an example: divide 35 by 8.

      In a way we turn it into a multiplication problem: what times 8 equals 35? So we know the 8, and use it to "double" -- but then to "halve", when 8 won't go evenly into 35:

      1	8
      2	16
      4	32	*
      1/2	4
      1/4	2	*
      1/8	1	*

      So the answer is 4+1/4+1/8

    • the Egyptians restricted themselves to the so-called "unit fractions", which are fractions of the form 1/m: unit fraction table, which is found on the Rhind Papyrus (which dates to around 1650 BCE).

      But they didn't restrict themselves to "halving", as our next example shows. Divide 6 by 7:

      1	7
      1/2	3+1/2	*
      1/4	1+1/2+1/4	*
      1/7	1
      1/14	1/2	*
      1/28	1/4	*

      So the answer is 1/2+1/4+1/14+1/28 (we usually order them from largest to smallest).

      Notice that the Egyptians didn't use decimals -- you shouldn't either!

      Why did Egyptians do things this way? (an example division problem, 3/5)

         Dominic Olivastro, "Ancient Puzzles", suggests a third reason why 
      this use of unary fractions is good. Consider the problem Ahmes poses 
      of dividing 3 loaves of bread between 5 people. We would answer "each
      person gets 3/5-ths of a loaf". If we implemented our solution, we might
      then cut 2 loaves into 3/5 | 2/5 pieces, with bread for 3 people; then
      cut one of the smaller pieces in half, giving the other two people 
      2/5 + 1/5 pieces. Mathematically acceptable, but try this with kids and
      they will insist that it is not an even division. Some have larger pieces,
      some have smaller.
      

      

      Ahmes would calculate 3/5 as :
         3/5 = ()3 + ()5 + ()15    [ = 1/3 + 1/5 + 1/15 ]
      Now cut one loaf into fifths, cut two more into thirds, then take one of
      the 1/3-rd pieces and cut it into 5-ths (for the 1/15-th pieces), and you
      can now distribute everyone's 3/5-ths share in a way that _looks_ equal,
      since they will have exactly the same size pieces. (And no, I don't want
      to argue about the crust.)
      

    • There is another way to get these answers, using the Fraudini trick and the Unit Fraction Table. So let's try those same examples but using the unit fraction table rather than our doubling tables.
      1. $\displaystyle \frac{35}{8}=\frac{32+2+1}{8}=4+\frac{1}{4}+\frac{1}{8}$

      2. \[ \displaystyle \frac{6}{7}=\frac{4+2}{7}=\frac{4}{7}+\frac{2}{7} =2\frac{2}{7}+\frac{2}{7} \]

         so we look up $\frac{2}{7}$, and find that $\frac{2}{7}=\frac{1}{4}+\frac{1}{28}$. Therefore,

         \[ \displaystyle \frac{6}{7}= 2*(\frac{1}{4}+\frac{1}{28})+\frac{1}{4}+\frac{1}{28}= \frac{1}{2}+\frac{1}{14}+\frac{1}{4}+\frac{1}{28} \]

      which is exactly what we got before -- except they're not in order from largest to smallest.

      

    • Here's a relatively easy one: Suppose Fatima had 3 loaves to share between 4 people. How would she do it? (Think about what the answer means, in terms of bread, and keeping kids happy.)

    • A little trickier:
      1. How would you divide 5 by 7?

         (Start with halves, and then what?)

      2. How can we use the unit fraction table to get the same answer?

    • How would you like to do story problems like this one?!