- My office hour Zoom for this afternoon will move to 5:00 because of a meeting.
-
- This session will be captured on Zoom, if I remember to turn it on, and record it.
- Our page of zooms and the play-by-plays.
- A reminder that you have an IMath
assignment due today, and a symmetry
assignment (which is now due next
Monday -- revised).
Plus some reading assignments....
- Our second exam is this Friday, 4/8. It will cover the following:
- Planar graphs and Euler's formula
- Euler Paths and Circuits
- Mayan numbers
- Babylonian numbers
- Egyptian multiplication and division
- Fibonacci numbers and spirals (from the Euclidean algorithm for finding the greatest common divisor)
- Fibonacci Nim
- Golden Rectangles and Spirals
- All readings. Just as before, I'll be asking some short answer questions, just to check if you've been doing the readings.
We'll be reviewing next time: come with your questions!
- Symmetry:
- Reflections
- Rotations
- Symmetry appears everywhere in nature. We'll see
three-dimensional versions of that today.
But Weyl's classic Symmetry gives us some beautiful examples (e.g. pages 59, 75).
Today we consider the Platonic solids, which possess a great deal of symmetry: they're super-symmetric solids.
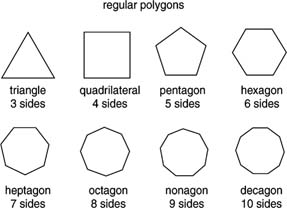
- We begin our discussion with the convex regular
polygons:
"A regular polygon is a polygon which is equiangular (all angles are equal in measure) and equilateral (all sides have the same length). Regular polygons may be convex or star."
- Last time we answered the following questions in the plane of 2-Dimensions:
- What is the most symmetric rectangle?
- What are regular polygons?
- How many regular polygons are there?
- What kinds of symmetry do they possess?
- Which regular polygons can be used to tile (tessellate) the plane?
- What could you do with a heptagon?
- As an example, consider regular convex hexagonal
graph paper, which represents a tiling of the plane by a
regular convex polygon. You see these kinds of tilings in bathrooms.
Bees have the same idea:

- The honeycomb is actually solid -- three-dimensional. The tubes
have hexagonal walls. But the comb is not Platonic.
A cube is an example of a Platonic solid. It's the one we're most familiar with, so let's start with that.
A Platonic solid is a solid for which
- All faces are congruent (identical) convex regular polygons, and
- Each face, each edge, and each vertex is exactly equivalent to every other face, edge, or vertex (respectively).
They're super-symmetric!
The Five Convex Regular Polyhedra (Platonic solids) -- thanks Wikipedia! Tetrahedron Hexahedron
or CubeOctahedron Icosahedron Dodecahedron 




fire earth air water universe - What do these have to do with Plato? According to Weyl, "Plato, in the
dialogue Timaeus, associates the regular pyramid, octahedron,
cube, icosahedron, with the four elements of fire, air, earth and water
(in this order), while in the pentagondodecahedron he sees in some sense
the image of the universe as a whole."
Some nice illustrations from Weyl's book.
- What's wrong with six sided polygons, and beyond? Consider the
hexagonal graph paper, of the tiling of the plane: why can't it be folded up
into a solid?
The answer involves Euler's formula, as Weyl discusses.
- What can you do with these solids?
- Play basketball? Three Sides to This Story: Knicks Dust Off
Phil Jackson's Triangle Offense, from the New York Times:

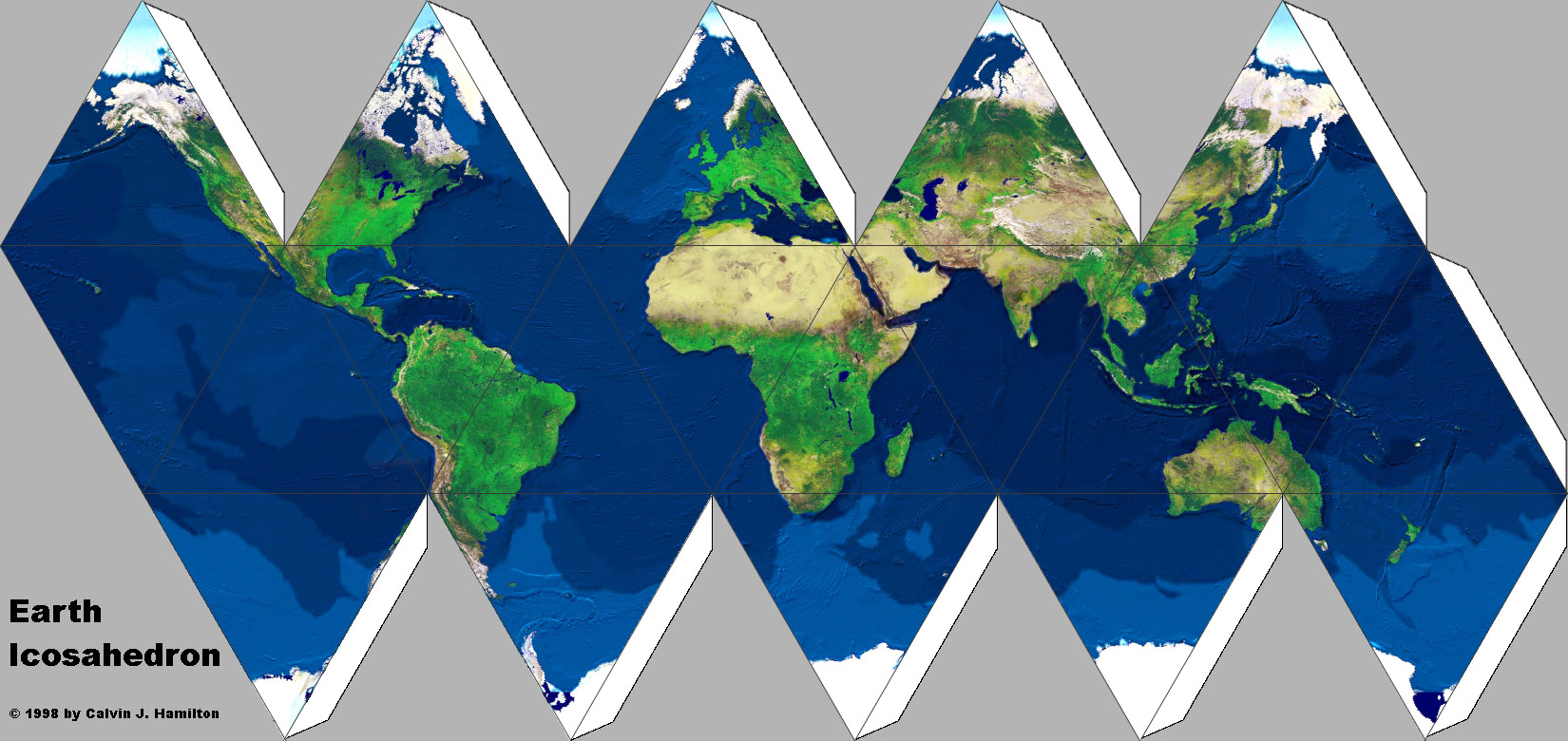
- Map the Earth?

The Platonic solids allow us to make "flat spheres" (sort of!):
- Johannes Kepler thought that the orbits of the planets (of which
five were known at the time) were somehow related to the various
Platonic solids, as shown in
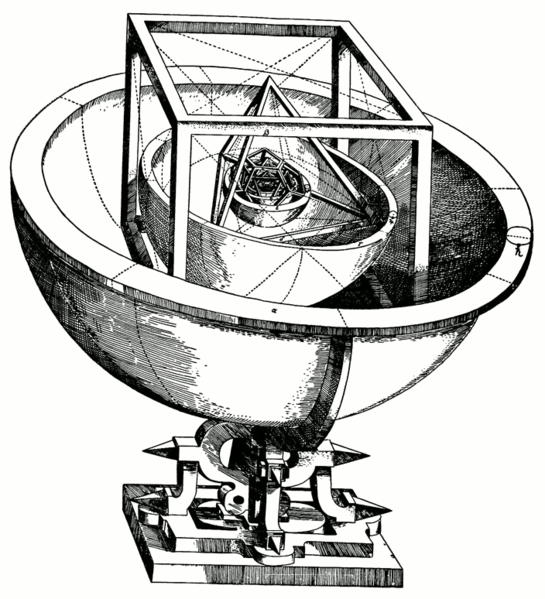
"The six spheres each corresponded to one of the planets (Mercury, Venus, Earth, Mars, Jupiter, and Saturn). The solids were ordered with the innermost being the octahedron, followed by the icosahedron, dodecahedron, tetrahedron, and finally the cube. In this way the structure of the solar system and the distance relationships between the planets was dictated by the Platonic solids."
And then Uranus was discovered, and there was not a sixth Platonic solid. And so science evolves....
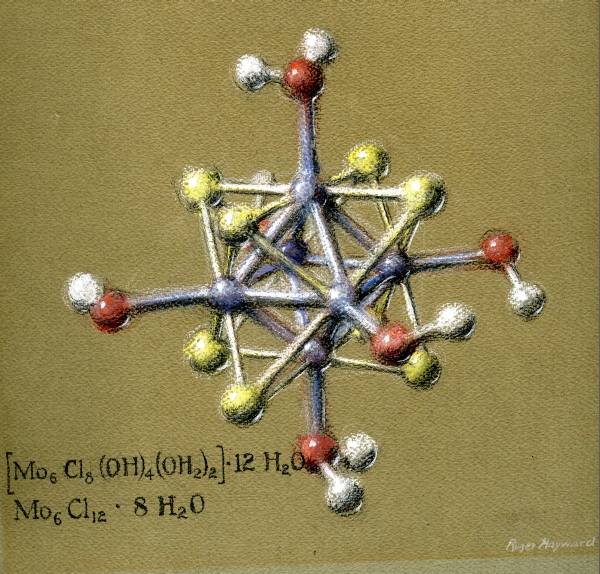
- Something interesting to share: great images from Linus Pauling's and Roger Hayward's The Architecture of Molecules (a book created especially for young people, and based off of Pauling's article in the 1964 Proceedings of the National Academy of Sciences.
From Pauling's paper:
Molecular architecture may be said to have originated in 1874, when J. H. van't Hoff and J. A. le Bel independently formulated the brilliant postulate that the four valence bonds of the carbon atom are directed approximately toward the corners of a regular tetrahedron. It was extended into inorganic chemistry in 1893, when A. Werner suggested that in many inorganic complexes six atoms are arranged at the corners of a regular octahedron about a central atom, and that other geometrical structures are represented by other complexes.These are some higher quality images than my scans:
- So what can you do with a dodecahedron? Look like a super-brainy, cool scientist!
From the October 7th, 2011 New York Times
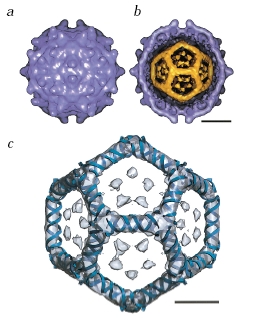
- Icosahedron
- Amoeboid protozoa Circogonia icosahedra:
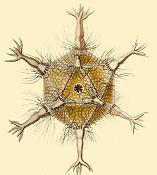
- Viruses:
- The Cliff Notes Version...

"An array of viruses. (a) The helical virus of rabies. (b) The segmented helical virus of influenza. (c) A bacteriophage with an icosahedral head and helical tail. (d) An enveloped icosahedral herpes simplex virus. (e) The unenveloped polio virus. (f) The icosahedral human immunodeficiency virus with spikes on its envelope."
- Bacteriophages and Virions
- The Cliff Notes Version...
- Dodecahedral
- Amoeboid protozoa Circogonia icosahedra:
- More critters:
- Play basketball? Three Sides to This Story: Knicks Dust Off
Phil Jackson's Triangle Offense, from the New York Times:
- Now let's use what we can deduce of Platonic solids to fill in the
following table:
# of Vertices Edges Faces faces at each vertex sides at each face Tetrahedron Cube Octahedron Dodecahedron Icosahedron What conclusions can we draw from this data? Is there a pattern? (Of course there is!:) The pattern leads to the concept of "Duality":
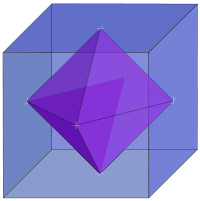
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.


Pastel drawing of a compound of Molybdenum Dichloride:
- Each Platonic solid has a "twin" -- called its dual -- which we can discover from the table.
- Symmetry, by Hermann Weyl (Princeton University Press, 1952)
- Symmetry of lifeforms on Earth
- A fun reading on symmetry
- Fibonacci
Spiral Fractal maker.
- How to win at Nim
- Unit Fraction Table
- How Egyptians wrote fractions.
- Problem 81: converting between different measures with fractions
- Egyptian fractions (Wikipedia)
- An amazing source for Egyptian Fraction info
- The new Mayan glyphs from Xultun, Guatemala: lots of spectacular calendar calculations, but nothing whatsoever about 2012 AD
- "Ancient Maya Astronomical Tables from Xultun, Guatemala". William A. Saturno, David Stuart, Anthony F. Aveni, Franco Rossi
- Part of the wall from which our Mayan tablet is taken